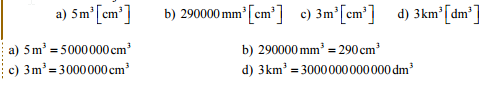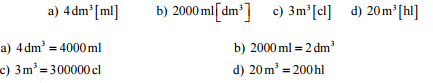Př. 1: Vyber z následujících vět ty, které hovoří o fyzikální síle. Pokud ve větě nejde o fyzikální sílu, nahraď ji jiným slovem.
a) Demokratické politické síly se opět nedohodly na společném postupu. b) Kupujte nový ExtraBěl s dvojnásobnou prací silou. c) Vzdušné síly NATO opět zaútočily na vojenské cíle. d) Nemám silnější prkno než 3 cm. e) Motory rakety Saturn V působily během startu silou 32 MN. f) „To je síla“, zařval Petr a vrhl se na dort.
Př. 2: Lidé často soutěží v tom, kdo má větší sílu. Soutěže o největšího siláka jsou daleko populárnější než soutěže o největšího, nejmenšího nebo nejvlasatějšího člověka. Zkus najít důvody, proč je (byla) síla pro lidi tak důležitá.
Př. 3: Popiš síly, které působí v následujících situacích. a) Zvedáme tašku s učením. b) Mačkáme houbu na tabuli. c) Tlačíme stůl před sebou. d) Táhneme sáňky.
Př. 4: Vymysli další situace, kdy Ty působíš na něco silou (nebo něco působí silou na Tebe).
Př. 5: Jaká skutečnost nám komplikuje sledování sil?
Př. 6: Prohlédni si video se sestřihem fotbalových parádiček. Co všechno může síla, kterou působí hráč na míč s míčem udělat? Existují nějaké další účinky síly, které z videa nejsou zřejmé, ale určitě i tam k nim dochází? V jaké situaci by tyto účinky byly viditelnější?
Př. 7: Vezmi si do ruky sirku. Zkus ji ulomit pouze hlavičku. Jak na ni musíš působit? Co při tom cítíš? Působíš silou pouze ty nebo i něco jiného? Zkus sirku zlomit na dvě poloviny. Porovnej situaci s ulamováním hlavičky. Zapiš svá pozorování do sešitu. Př. 8: Stoupni si mimo lavici a vezmi do ruky svou školní tašku. Stůj s taškou v ruce normálně. Jaké síly při tom působí? Zvedni ruku tak, aby si je měl vodorovně.
Změnilo se něco? Jak je cítit síla, kterou taška působí na tvou ruku? Zvedni ruku s taškou nad hlavu, tak aby ruka byla kolmo. Jak působí síly v této poloze? Pokud je Tvá taška příliš těžká vyndej část věcí na lavici. Domácí bádání: Každá fyzikální síla musí splňovat tří podmínky (podobně například jako auto označujeme předmět, který má čtyři kola, motor, brzdy, …). Projdi všechny popisy sil v hodině a zkus tyto tři podmínky, které všechny síly splňují najít.
Žáci přinesou příště: dvě gumičky