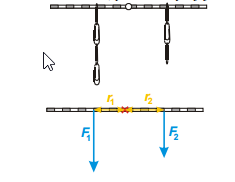
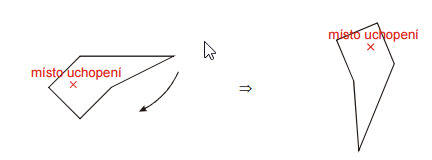Pomôcky: valcové závažia 100 g, podložky s rôznym koeficientom trenia.

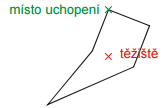
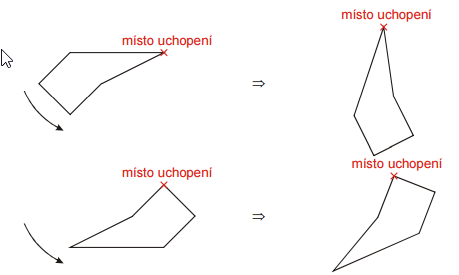
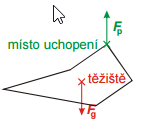
Keď sme v minulej hodine prevádzali pokusy s ústrižkom, ústrižok sa medzi prstami vždy natočil rovnakým spôsobom do rovnakej polohy. V tejto polohe, v ktorej samovoľne zostával, bola nulová ako výsledná sila tak výsledný moment všetkých síl, ktoré na ústrižok pôsobili. Takej polohe hovoríme stála (stabilná) rovnovážna poloha (predmet je v nej v rovnováhe a samovoľne sa do nej pri malom vychýlení vracia).

Rovnovážna poloha stála (stabilná)

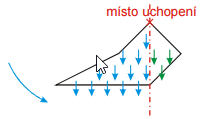
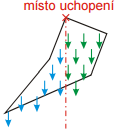
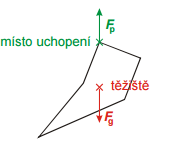
Pr. 1: Okrem rovnovážnej polohy, do ktorej sa ústrižok samovoľne překlápěl, existuje (skôr teoreticky) ešte jedna rovnovážna poloha ústrižku držaného medzi prstami. Aká? Prečo pri reálnych pokusoch v tejto polohe ústrižok nedrží?

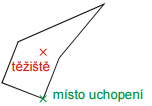
Rovnovážna poloha vznikne aj v prípade, že výstrižok zo stálej rovnovážnej polohy otočíme o 180 °. Ťažisko potom bude presne nad miestom uchopenia.
V reálnych pokusoch v tejto polohe ústrižok nedrží, pretože pri najmenšom vychýlenie sa ústrižok prevráti do stálej rovnovážnej polohy. Takéto rovnovážnej polohe hovoríme vratká (labilné) rovnovážna poloha. Ak chceme predmet umiestniť tak, aby nespadol, nemá labilný poloha praktický význam (aj najslabší vánok by predmet z rovnovážnej polohy zhodil).
Pr. 2: Sleduj učiteľa, ako sa snaží udržať metla na špičke prsta. Prečo je to tak ťažké? Ako by sme museli metlu držať, aby to bolo jednoduché?
Balancovanie s metlou je ťažké, pretože sa snažím ho udržať vo vratkej rovnovážnej polohe ⇒ metlu z nej neustále padá ⇒ musíme neustále meniť miesto, kde metlu podopierame a strkať miesto podopieranie pod ťažisko.
Ľahké je udržať metlu v stabilnej rovnovážnej polohe (s ťažiskom pod miestom uchytenia (v tomto prípade je metla fakticky zavesené).

Pr. 3: Nájdi príklad, kedy človek zotrváva v labilná rovnovážnej polohe. Čo mu pomáha z nej nespadnú?
V takmer labilná polohe zotrvávame napríklad pri jazde na bicykli. Na stojacom bicykli rýchlo spadneme ⇒ udržať rovnováhu nám pomáha:
• rotácie kolies (kolesá nechcú zmeniť smer otáčania a tým bráni spadnem, pri ktorom by sa smer otáčania zmenil),
• pohyb vpred nám umožňuje neustále meniť miesto, kde sa podopierame, ako pohyb ruky umožňoval balansovať s metlou.
Pokiaľ na bicykli nejdeme, bez vonkajšej opory sa neudržíme (pretekári v týchto disciplínach udržujú rovnováhu neustálym poskakovaním s kolesom, ktoré im umožňuje neustále meniť
miesto, kde sú podopretá).
Pr. 4: Vysvetli, prečo sa lamos konštrukcia stojí na špičke ihly a nepadá.
Vidličky v konštrukcii smerujú nadol a sú ďaleko ťažšie ako korok ⇒ ťažisko celej konštrukcie je pod špičkou ihly, na ktoré konštrukcie stoja ⇒ ťažisko je pod bodom podopretie ⇒ konštrukcie nestojí na špičke v labilné polohe, ale je zavesená vo stabilnú rovnovážnej polohe (a teda sa po vychýlenie vráti späť).
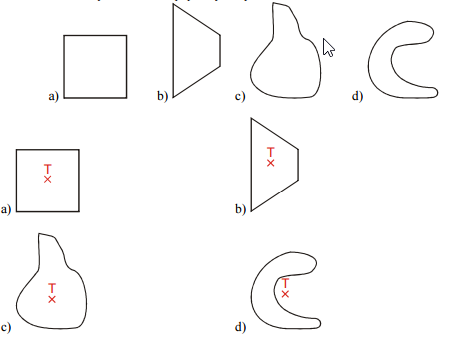
Pr. 5: Na obrázku je nakreslené profil. V ktorých miestach je gulička v stabilnej rovnovážnej polohe? Sú všetky tieto polohy rovnako dobré (rovnako stabilný)? ktorá z nich je najstabilnejší? Ktorá najmenej stabilné? Prečo? Čo by sme mohli považovať za
mieru stability rovnovážnej polohy?

Na profile sú tri miesta, v ktorých je gulička v stabilnej rovnovážnej polohe.

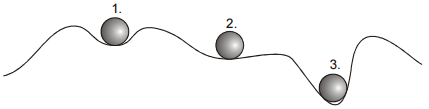
Najstabilnejší polohou je poloha 3, najmenej stabilný je poloha 2. U polohy 2 stačí malé postrčenie a guľôčka sa zakotúľa inam, naopak v mieste 3 je treba do guľôčky veľa strčiť.
Mierou stability by mohla námaha nutná na premiestnenie guľôčky z rovnovážnej polohy.
Dodatok: Náhradou námahy je vo fyzike práce alebo energie, preto sa hovorí, že stabilita zodpovedá prácu, ktorú musíme vykonať, aby sme predmet z rovnovážnej polohy dostali.

Pr. 6: Do koľkých rovnovážnych polôh môžeme položiť kváder na lavici. Ktorá z nich je najstabilnejšie? Čo sa musí stať, aby sa kváder preklopil do inej rovnovážnej polohy?
Kváder môžeme položiť do troch rovnovážnych polôh (kváder má tri rôzne steny). najstabilnejší je poloha, pri ktorej kváder stoja na najväčšiu stene.
Do inej rovnovážnej polohy musíme kocku preklopiť cez jednu z hrán (v jednom okamihu sa ťažisko dostane nad hranu, o ktorú sa kváder v tomto okamihu opiera.
Pr. 7: Na obrázku je doska stola a jedna noha (pohľad zhora). Akým spôsobom môžeme dosku podoprieť ak máme k dispozícii:

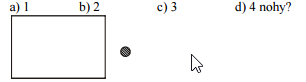
Ako umiestniť štyri nohy stola tak, aby bol najstabilnejší?
Vo všetkých prípadoch platí, že ťažisko stola musia byť podložené bud priamo jednou z nôh alebo viac nohami (keď sa nachádza „medzi nimi“).
a) jedna noha

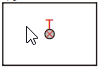
Ťažisko stola musí byť priamo nad nohou.
b) dve nohy

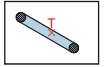
Ťažisko stola môže byť nad modro vyfarbenou plochou medzi nohami.
c) tri nohy

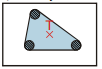
Ťažisko stola môže byť nad modro vyfarbenou plochou medzi nohami.
d) štyri nohy

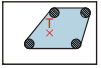
Ťažisko stola môže byť nad modro vyfarbenou plochou medzi nohami.
Najvýhodnejšie je umiestniť nohy do štyroch rohov stola. Ťažisko stola tak môže byť kdekoľvek na jeho doske.

Pr. 8: Prečo má laboratórne stojan širokú základňu z kovu?
Široká základňa – veľká plocha, nad ktorou môže byť ťažisko zaveseného predmetu. Kovová základňa – kov je ťažký, preto ovplyvňuje spoločné ťažisko zaveseného predmetu a stojanu, ktoré musia byť nad základňou.
Pr. 9: Človek, ktorý nesie vedro plný vody, sa nakláňa na stranu. Na ktorú? Prečo? Nakláňa sa na opačnú stranu než v ktorej má vedro, inak by ťažký kýbel s vodou posunul jeho ťažisko príliš do strany.
Pr. 10: Postavte sa ľavým ramenom tesne k stene a zdvihni pravú nohu. Čo sa deje? Prečo? Čo sa stane, keď zvedneš ľavú nohu? Prečo? Zdvihnutie pravej nohy ⇒ padáme doprava od steny. Nie sme podopretie pod ťažiskom (ťažisko je medzi nohami, stojíme len na ľavej) ⇒ pôsobí na nás nenulový moment sily ⇒ začneme sa otáčať (a padať).
Zdvihnutie pravej nohy ⇒ nič sa nedeje. V skutočnosti je situácia skoro rovnaká ako v predchádzajúcom bode. Padáme doľava k stene. Nie sme podopretie pod ťažiskom (ťažisko je medzi nohami, stojíme len na ľavej) ⇒ pôsobí na nás nenulový moment sily ⇒ začneme sa
otáčať (a padať). Pretože ihneď narazíme na stenu, ktorá na nás ihneď začne pôsobiť silou a tým moment vyrovná, pád sa ihneď zastaví.
Pr. 11: Ako sa zmení Tvoj postoj, keď nesieš na chrbte veľmi ťažký batoh? Prečo? Podobná situácia ako pri nosení vody. Snažíme sa udržať ťažisko (spoločné ťažisko nás a batohu) na normálnom mieste ⇒ batoh vzadu na chrbte vyrovnáme tým, že sa nakloníme dopredu.
Pr. 12: Človek s veľkým pivným bruchom (človek pivný čiže homo cerevisiae) tiež nechodia úplne vzpriamene. Prečo?
Opačná situácia ako v minulom bode. Veľké brucho posúva ťažisko dopredu ⇒ homo cerevisiae sa musí zakloniť, aby zmenu vyrovnal.

Pr. 1: Do korkovej zátky je zapichnutý ihla a dve vidličky. Vysvetli, prečo stojí na druhej ihle zapichnuté v druhom korku a nespadne.
Pr. 2: Vezmi do ruky papierový útvar. Uchop ho na kraji pevne medzi prstami tak, aby zvyšok útvaru trčal vodorovne od miesta uchopenie. Pomaly prsty uvoľňuj tak, aby sa útvar mohol medzi prstami otáčať, ale zároveň z nich úplne nevypadol. Čo sa deje? opakuj pokus s tým, že na začiatku uchopíš útvar medzi prstami v inom mieste. Zmení sa niečo, keď nebudeš držať útvar na okraji. Vysvetli pohyb útvaru.
Pr. 3: V ktorom mieste musíme papierik uchopiť, aby sa nezhoupnul?
Pr. 4: Zostav postup na hľadanie ťažisko predmetov uchopovaním medzi prstami.
Pr. 5: Vymeň si papierik so susedom a nájdi jeho ťažisko bez toho, aby si ho uchopoval medzi dva prsty, nechával ho zosunúť a kreslil na neho vertikály.
Pr. 6: Vezmi do ruky pero a postáv si ju na jeden prst. Nakresli jej obrázok a do neho sily, ktoré na nej pôsobia.
Pr. 7: Nakresli podobný obrázok ako v predchádzajúcom príklade pre prípad, že by si pero podložil mimo ťažiska.
Pr. 8: Nakresli obrázok svojho ústrižku v okamihu, keď si ho držal medzi prstami on sa už ustálil. Do obrázku dokresli sily, ktoré na neho pôsobia (gravitáciu nakresli ako jednu silu). Prečo gravitačná sila nespôsobí v tejto polohe otočenia ústrižku? nakresli rovnaký obrázok pre situáciu, keď je papierik v polohe, z ktorej sa rozkýva.
Pr. 9: Odhadni polohu ťažiska papierových výstrižkov.

Pr. 10: Kde leží ťažisko u človeka? Navrhni pokusy, ktoré by umožnili Tvoj odhad overiť.
Pr. 11: Ako ďaleko môžeme vysunúť krabičku od zápaliek zo stola, bez toho aby spadla na zem?
Pr. 12: Vysvetli, prečo krabička neprepadol, aj keď sme ju vysunuli do viac ako polovice podstavy. Čím si svoj odhad môžeš overiť, bez toho aby si sa do nej pozrel?
Pr. 13: V roku 1968 vyhral olympijské hry v skoku vysokom Dick Fosbury s novým štýlom nazývaným flop. Pozri si spomalené zábery skoku flopom, porovnaj ich s predchádzajúcom štýlom straddle a vysvetli, prečo flop umožňuje skokanom skákať vyššie.

Pomôcky: kartónové obrazce na hľadanie ťažisko, vidlička-korky-ihla-div,
Pr. 1: Do korkovej zátky je zapichnutý ihla a dve vidličky. Vysvetli, prečo stojí na druhej ihle zapichnuté v druhom korku a nespadne.
Pr. 2: Vezmi do ruky papierový útvar. Uchop ho na kraji pevne medzi prstami tak, aby zvyšok útvaru trčal vodorovne od miesta uchopenie. Pomaly prsty uvoľňuj tak, aby sa útvar mohol medzi prstami otáčať, ale zároveň z nich úplne nevypadol. Čo sa deje? opakuj pokus s tým, že na začiatku uchopíš útvar medzi prstami v inom mieste. Zmení sa niečo, keď nebudeš držať útvar na okraji. Vysvetli pohyb útvaru. Bez ohľadu na to, v ktorom mieste útvar uchopíme sa útvar rozkýva tak, aby bol útvar pod miestom, v ktorom ho držíme.

Ak útvar nedržíme uprostred, rozkýva sa aj v prípade, že ho nedržíme na okraji.

Papierik sa rozkýva, pretože chce byť čo najnižšie (veci padajú dole kvôli gravitácii). Na správanie papieriku sa môžeme pozrieť aj pomocou rovnováhy na páke. V mieste, kde papierik držíme je os otáčania. Na každý kúsok papierika potom pôsobí malá gravitačná sila (v úplnej väčšine prípadov si pôsobenie gravitácie predstavujeme ako jedinú silu na celý papierik. Vo skutočnosti pôsobí Zem na každý kúsok papiera zvlášť a celková gravitačná sila je súčtom týchto malých síl).

Z obrázku je vidieť, že síl, ktoré sa snažia pootočiť papierik proti smeru hodinových ručičiek je ďaleko viac (a s ďaleko väčším momentom) než síl, ktoré sa snažia otočiť papierik opačným
smerom ⇒ papierik sa otáča proti smeru hodinových ručičiek kým sa celkové momenty na oboch stranách nevyrovnajú.

Nakreslíme si na papierik niekoľko zvislých čiar, ktoré ho po preklopení rozdeľujú dve rovnako silné (Z hľadiska otáčania) časti.

Všetky prechádzajú (to u viac ako dvoch priamok nie je samozrejmé) jedným bodom, ktorý sa nazýva ťažisko.
Pr. 3: V ktorom mieste musíme papierik uchopiť, aby sa nezhoupnul?
Papierik musíme uchopiť v ťažisku.
Pr. 4: Zostav postup na hľadanie ťažisko predmetov uchopovaním medzi prstami.
• Uchopíme predmet medzi dva prsty a necháme ho pretočiť do rovnovážnej polohy.
Nakreslíme na predmet zvislú priamku od miesta, kde ho držíme.
• Zopakujeme predchádzajúceho krok s tým, že predmet držíme v inom mieste.
• Bod, v ktorom sa obe zvislé priamky pretnú, je ťažiskom.
Pr. 5: Vymeň si papierik so susedom a nájdi jeho ťažisko bez toho, aby si ho uchopoval medzi
dva prsty, nechával ho zosunúť a kreslil na neho vertikály.
Skúšame pokladať papierik na prst, ak sa neprevráti, je podopretý pod ťažiskom.
Pr. 6: Vezmi do ruky pero a postáv si ju na jeden prst. Nakresli jej obrázok a do neho sily, ktoré na nej pôsobia. Prepisku musíme postaviť tak, aby jej ťažisko bolo nad miestom, kde sa dotýka prsta.

Sily, ktoré pre pero pôsobia majú:
• nulovú výslednicu (preto propiska stojí),
• nulový výsledný moment otáčania (preto sa prepisovačka neotáča).
Dodatok: V skutočnosti nemajú sily v predchádzajúcom případku (ani v iných situáciách s nulovú výslednicou a nulovým výsledným momentom) nulový moment len vzhľadom k osi prechádzajúcej bodom, kde sa pero dotýka ruky, ale voči ľubovoľnému iné osi otáčania.
Pr. 7: Nakresli podobný obrázok ako v predchádzajúcom príklade pre prípad, že by si pero podložil mimo ťažiska.

Moment gravitačné sily vzhľadom k osi v bode, kde sa dotýka propiska prsta, nie je nulový ⇒ ceruzka sa začne otáčať a spadne z prsta.
Pr. 8: Nakresli obrázok svojho ústrižku v okamihu, keď si ho držal medzi prstami on sa už ustálil. Do obrázku dokresli sily, ktoré na neho pôsobia (gravitáciu nakresli ako jednu silu). Prečo gravitačná sila nespôsobí v tejto polohe otočenia ústrižku? nakresli rovnaký
obrázok pre situáciu, keď je papierik v polohe, z ktorej sa rozkýva.

Súčet oboch síl je nulový, rovnako ako výsledný moment (obe sily ho majú vzhľadom k osi prechádzajúce miestom uchopenia nulový).

Gravitačná sila má vzhľadom k osi prechádzajúcej miestom uchopenia nenulový moment ⇒ otočí papierikom tak, aby sa ústrižok dostal priamo pod ťažisko.
Ťažiskom nazývame myslený bod, v ktorom zdanlivo pôsobí gravitačná sila, pôsobiaca na predmet. ⇒
• Keď predmet uchopíme medzi dva prsty v ťažisku, tak sa nezhoupne (gravitačná sila má nulové rameno a nemá otáčavý účinok).
• Keď predmet podoprieme pod ťažiskom, tak zostane v pokoji (gravitačná sila má nulové rameno a nemá otáčavý účinok).
• Keď predmet uchopíme medzi dva prsty z ťažiska, tak sa rozkýva tak, aby ťažisko bolo pod miestom, kde predmet držíme (gravitačná sila má nulové rameno a nemá otáčavý účinok).
Pr. 9: Odhadni polohu ťažiska papierových výstrižkov.Ťažisko môže ležať aj mimo predmet.
Pr. 10: Kde leží ťažisko u človeka? Navrhni pokusy, ktoré by umožnili Tvoj odhad overiť. Ťažisko stojaceho človek a sa nachádza približne v úrovni pásu uprostred tela.
Overenie:
• Skúsime človeka ležiaceho na chrbte zdvihnúť v mieste, ku predpokladáme ťažisko. Ak sa trafíme, človek sa nevychyluje.
• Človeka ležiaceho na chrbte na lavici. Postupne sťahujeme dole, vo chvíli, keď sa s ním lavice začne preklápať, sa jeho ťažisko nachádza na hrane stola (kým je ťažisko nad doskou stola, sú zaťažované oba páry nôh. Ako milo sa ťažisko človeka ocitne na jednom okraji, druhú dvojicu nohou nič nezaťažuje a tak sa začne dvíhať.
Pr. 11: Ako ďaleko môžeme vysunúť krabičku od zápaliek zo stola, bez toho aby spadla na zem? Krabičku môžeme zo stola vysúvať dokiaľ bude podopreté jej ťažisko (leží uprostred krabičky) ⇒ krabičku môžeme vysunúť takmer z polovice.
Pr. 12: Vysvetli, prečo krabička neprepadol, aj keď sme ju vysunuli do viac ako polovice podstavy. Čím si svoj odhad môžeš overiť, bez toho aby si sa do nej pozrel? V krabičke je zrejme umiestnený na strane, ktorá zostala nad stolom, ťažký predmet. ťažisko krabičky sa tak posunulo z prostriedku krabička k tomu okraju.
Skontrolovať to môžeme tým, že krabičku dáme na stôl a začneme ju posúvať von obrátene než v pôvodným pokusu. Teraz by mala spadnúť ešte skôr než ju vysunieme z polovice.
Pr. 13: V roku 1968 vyhral olympijské hry v skoku vysokom Dick Fosbury s novým štýlom nazývaným flop. Pozri si spomalené zábery skoku flopom (3:00), porovnaj ich s predchádzajúcom štýlom straddle (0:19) a vysvetli, prečo flop umožňuje skokanom
skákať vyššie.
Pri skoku flopom má skokan nohy pod latkou do okamihu, keď sa mu podarí pod latku strčiť ruky ⇒ jeho ťažisko sa nemusí presunúť cez latku (ťažisko človeka, ktorý robí most je tiež pod jeho bruchom).
Pri skoku straddle sa v jednom okamihu celé telo skokana nachádza nad latkou ⇒ počas skoku musí skokan dostať ťažisko nad latku.
Odraz rozhoduje o tom, ako vysoko sa nám podarí dostať naše ťažisko. Výhodnejšie je štýl skoku, ktorý nás nenúti zdvíhať ťažisko tak vysoko. Pri rovnako intenzívnom odrazu, je pri flope
možné skočiť väčšiu výšku.
Vysvetlenie https://www.youtube.com/watch?v=RaGUW1d0w8g (2:38).
Zhrnutie: Ťažisko je myslený bod, v ktorom sa zdanlivo sústreďuje hmotnosť predmetu.

Pr. 1: Sformulujte obe pravidlá pre rovnováhu na hojdačke pomocou vyššie uvedených fyzikálnych pojmov.
Pr. 2: prekreslí situáciu schematicky do zošita (bez sponiek a špendlíka). V obrázku vyznač os otáčania, pôsobiace sily a ich ramená. Je páka v rovnováhe?

Pr. 3: Na páku pôsobia dve sily. Zapíš podmienku pre rovnováhu pomocou rovnice.

Pr. 4: Zapíš rovnicou podmienku pre rovnováhu na páke na obrázku.

Pr. 5: Prečo sa kľučka montuje na dvere vždy čo najďalej od pántov. Čo by sa stalo, keby bola kľučka na druhom konci dverí (u pántov).
Pr. 6: Hojdačka je dlhá 3 m a je podložená uprostred. Amálka vážiaci 25 kg si sadne na jeden koniec. Ako ďaleko od stredu si musí na druhej strane sadnúť otecko vážiaci 80 kg, aby bola hojdačka vyvážená?
Pr. 7: Páka na obrázku je v rovnováhe. Vypočítajte veľkosť sily F.

Pr. 8: Veľmi nebezpečné je strkať k pántom dvere. Čo v takom prípade hrozí? Akú silou by dvere na prsty na pántov pôsobili, keby na druhej strane niekto zatváral silou 10 N?

Pomôcky: špejlová hojdačka
Pedagogická poznámka: Na začiatku hodiny kontrolujeme pravidlá, ktoré mali žiaci sformulovať za domácu úlohu. Ich formulácia nemusí byť rovnaká ako formulácia učeníci, ale mala by byť správna a zrozumiteľná. Žiaci čítajú svoje pravidlá pred triedou a trieda je
kontroluje. Kontrola pravidiel z minulej hodiny.
Ak máme na oboch stranách len jednu skupinu sponiek, platí: Súčin počtu sponiek a počtu dielov na oboch stranách je rovnaký.
Ak je na jednej zo strán viacerých skupín sponiek, platí (všeobecnejšie pravidlo): Pre obe strany sčítame súčiny počtov sponiek a počtov dielikov a obaja súčty musia byť rovnaké.
Ako o rovnováhe na hojdačke hovorí fyzici?
• Celú hojdačku označujeme ako páku.
• Špendlík, okolo ktorého sa hojdačka otáča, (presnejšie priamku, prechádzajúcej stredom špendlíka) označujeme ako os otáčania (ide o jedinú časť párky, ktorá sa pri otáčaní nepohybuje).
• Sponky na páku pôsobí silou (značka F).
• Vzdialenosť pôsobiska sily od osi otáčania sa nazýva rameno sily (väčšinou značka r alebo d).
• Súčin veľkosti sily a ramena sily (ktorý rozhoduje o rovnováhe) sa nazýva moment sily (značka M). Jednotkou momentu sily je Newton meter [N * m].
Dodatok: Pretože veličinu moment sily sme zaviedli ako súčin sily a vzdialenosti, aj jej jednotku sme získali ako súčin jednotky sily a jednotky vzdialenosti. Tento postup sa vo fyzike používa veľmi často a užitočne obmedzuje množstvo jednotiek.
Pr. 1: Sformulujte obe pravidlá pre rovnováhu na hojdačke pomocou vyššie uvedených fyzikálnych pojmov.
Ak máme na oboch stranách len jednu skupinu sponiek, platí: Momenty síl na oboch stranách páky sú zhodné. Ak je na jednej zo strán viacerých skupín sponiek, platí (všeobecnejšie pravidlo): Súčet momentov síl na jednej strane sa rovná súčtu momentov síl na druhej strane.

Pr. 2: prekreslí situáciu schematicky do zošita (bez sponiek a špendlíka). V obrázku vyznač os otáčania, pôsobiace sily a ich ramená. Je páka v rovnováhe?

Os otáčania je vyznačená červeným krížikom.
Páka nie je v rovnováhe:
• moment sily vľavo je 4 * 4 = 16,
• moment sily vpravo je 3 * 5 = 15,
Páka sa nakloní ľavou stranou nadol.
Pr. 3: Na páku pôsobia dve sily. Zapíš podmienku pre rovnováhu pomocou rovnice.

Momenty oboch síl sa musí rovnať: M M 1 2 =.
Dosadíme za momenty síl: F1r1 = F2r2.
Pr. 4: Zapíš rovnicou podmienku pre rovnováhu na páke na obrázku.

Celkový moment vľavo sa musí rovnať celkovému momentu vpravo: M1 = M2 + M3.
Dosadíme za momenty síl: F1r1 =  F2r2 +F3r3.
Pr. 5: Prečo sa kľučka montuje na dvere vždy čo najďalej od pántov. Čo by sa stalo, keby bola kľučka na druhom konci dverí (u pántov).
Čím ďalej od pántov pôsobíme silou, tým väčšia je moment sily, ktorým dvere otvárame a tým ľahšie sa dvere otvárajú. Keby bola kľučka na u pántov, moment sily, ktorú dvere otvárame by bol ďaleko menší a museli by sme tlačiť väčšou silou.
Pedagogická poznámka: O hodine si to vyskúšať nestíhame (púšťam k dverám tých, ktorí spočítajú nasledujúce príklady), všetci zostávajúci majú za úlohu si to vyskúšať o prestávke alebo doma.
Pr. 6: Hojdačka je dlhá 3 m a je podložená uprostred. Amálka vážiaci 25 kg si sadne na jeden koniec. Ako ďaleko od stredu si musí na druhej strane sadnúť otecko vážiaci 80 kg, aby bola hojdačka vyvážená? Ide o rovnakú situáciu ako v prípade 3 ⇒ obe sily by na páku pôsobiť rovnakým momentom. Amálka aj otecko pôsobí na hojdačku silou, ktorá sa rovná gravitačnej sile Zeme.

Otecko si musí sadnúť 0,47 m od stredu hojdačky.
Pr. 7: Páka na obrázku je v rovnováhe. Vypočítajte veľkosť sily F.

Momenty síl na pravej strane nemôžeme sčítať, pretože obe sily majú opačný smer a snaží sa otáčať páku opačným smerom (sila 30 N otáča páku rovnakým smerom ako sila F). Celkový moment na pravej strane: 1,5 * 40 – 0,5 * 30 N * m = 45 N * m.
Pre ľavú silu musí platiť: F * 1,25 = 45.
Sila F musí mať veľkosť 36 N.
Pr. 8: Veľmi nebezpečné je strkať k pántom dvere. Čo v takom prípade hrozí? Akú silou by dvere na prsty na pántov pôsobili, keby na druhej strane niekto zatváral silou 10 N?
Dvere budú privierať prstami (a stláčať je), kým prsty na nich nebudú pôsobiť rovnako veľkým momentom ako sila, ktorú niekto zatvára dvere ⇒ potrebujeme zmerať ramená oboch síl.
• Rameno sily otvárajúce dvere: 70 cm.
• Rameno sily pôsobiace na prsty: 2 cm.
Na prsty privreté v u pántov pôsobí sila 350 N.
Zhrnutie: Páka je v rovnováhe, keď v oboch smeroch pôsobí rovnaký celkový moment sily.