Pr. 1: Aké vlastnosti má najjednoduchšie pohyb?
Pr. 2: Nájdi predmety, ktoré sa pohybujú rovnomerne priamočiaro.
Pr. 3: Navrhni prakticky realizovateľný postup, ako s triedou študentov zmerať čo najpresnejšie pohyb idúceho autíčka.

Pr. 4: Urči rýchlosti (s presnosťou na jedno desatinné miesto) autíčka v jednotlivých intervaloch a doplň ich do tabuľky.
Pr. 5: Nájdi niektoré z príčin, ktoré mohli spôsobiť nepresnosti pri meraní dráhy vozíka a vyústiť do rozdielnych hodnôt rýchlosti v jednotlivých intervaloch.
Pr. 6: Pozri si tabuľku s vypočítanými hodnotami rýchlosti a odhadni, ktorá z hodnôt
dráhy bola zrejme zmeraná zle a aká mala byť jej skutočná hodnota.

Pr. 7: Nájdi vlastnosť, podľa ktorej je možné rozoznať rovnomerný pohyb už z hodnôt dráhy bez počítania rýchlosťou.
Pr. 8: Ako bude vyzerať graf závislosti dráhy vozíka na čase? Ako bude vyzerať graf závislosti rýchlosti na čase? Zakreslite obaja odhady do jedného obrázku.
Pr. 9: Nakresli na milimetrový papier do jedného grafu závislosť dráhy na čase (os na ľavej strane) a závislosť rýchlosť na čase (os na pravej strane). Pred nanášaním hodnôt si rozmysli všetky merítka tak, aby si čo najlepšie využil plochu grafu. Čím sa vyznačuje graf závislosti dráhy rovnomerného pohybu na čase? Čím sa vyznačuje graf rýchlosti rovnomerného pohybu na čase?

Pomôcky: autíčko, pásmo, zápalky (kriedy alebo iné značky), milimetrové papiere
Pr. 1: Aké vlastnosti má najjednoduchšie pohyb?
Najjednoduchším pohybom sa pohybuje predmet, ktorý:
• má stále rovnakú rýchlosť,
• ide po priamke (priamočiaro).
Pohyb sa stále rovnakou rýchlosťou označujeme ako rovnomerný pohyb. Ak rovnomerný pohyb prebieha po priamej trajektórii, nazýva sa rovnomerný priamočiary pohyb.
Pr. 2: Nájdi predmety, ktoré sa pohybujú rovnomerne priamočiaro.
Väčšina predmetov sa pohybuje nerovnomerne, rovnomerne priamočiaro sa pohybuje:
• auto na rovnom úseku prázdne diaľnice,
• niektoré hračky (autíčka bez ovládania),
• kozmickej sondy letiaci mimo slnečnú sústavu,
• kosačka na trávu na kosenie,
• …
Pre naše skúmanie použijeme autíčko na batérie určené na fyzikálne pokusy.
Pr. 3: Navrhni prakticky realizovateľný postup, ako s triedou študentov zmerať čo najpresnejšie pohyb idúceho autíčka.
Rovnako ako u slimáka nebudeme schopní zabezpečiť okamžité odčítanie hodnôt jedným človekom ⇒ jeden študent hlási časy merania, ostatní študenti rozmiestnenie pozdĺž predpokladanej dráhy pokladajú značky alebo rovno odpočítajú hodnoty podľa nastaveného metra.
V nasledujúcej tabuľke sú hodnoty, ktoré sme získali pri meraní rovnomerného pohybu autíčka na baterky.

Pr. 4: Urči rýchlosti (s presnosťou na jedno desatinné miesto) autíčka v jednotlivých intervaloch a doplň ich do tabuľky.

Divné: Hračka sa síce pohybovala rovnomerne, ale hodnoty rýchlosti nie sú všetky rovnaké !!
Fakt, že hodnoty rýchlosti nie sú rovnaké, neznamená, že sa vozík nepohyboval rovnomerne. Všetky namerané hodnoty, sú vždy zaťažené chybou a preto nemôžeme očakávať, že by hodnoty rýchlosťou vyšli rovnaké.
Pr. 5: Nájdi niektoré z príčin, ktoré mohli spôsobiť nepresnosti pri meraní dráhy vozíka a vyústiť do rozdielnych hodnôt rýchlosti v jednotlivých intervaloch.
Niektoré z možných príčin nepresností:
• zlé odpočítaní času na stopkách,
• zlé hlásenie času,
• neskoré alebo unáhlené reakcie na nahlásený čas,
• nepresné položenie značky,
• zlé odpočítaní dráhy,
• …
Z predchádzajúceho je zrejmé, že nie je možné očakávať, že by pri takto nepresne meranom pokuse vyšli všetky hodnoty rýchlosti rovnaké. Ak by sme merali presnejšie, hodnoty rýchlostí by
sa od seba líšili menej, ale presne rovnaké hodnoty nie je možné očakávať nikdy.
Jednou z najdôležitejších častí fyziky je metodika, ktorá sa zaoberá meraním a výpočtom chýb. Pri naozajstných vedeckých pokusoch sa vždy určuje aj veľkosť chyby merania, aby bolo možné odhadnúť, čo je ešte reálny jav, a čo už je odchýlka spôsobená chybou.
Rovnomerný pohyb sa vyznačuje tým, že rýchlosti vo všetkých intervaloch sú približne rovnaké (miera přibližnosti, ktorú je ešte možné akceptovať, závisí od podmienok a presnosti merania).
Pedagogická poznámka: Predchádzajúci diskusie je pre budúcnosť výučby fyziky úplne zásadné.
Študenti bývajú počas svojho vzdelávania spravidla veľmi málo konfrontovaní s pokusmi a už len veľmi zriedka s meraním. Fyzikálne deje (ale všeobecne všetky predmety) sú im predkladané v značne zidealizované podobe, s ktorou sa v živote nikdy nestretnú a tak
dospievajú k názoru, že látka, ktorú sa učia v škole, nemá s realitou nič spoločné.
Pr. 6: Pozri si tabuľku s vypočítanými hodnotami rýchlosti a odhadni, ktorá z hodnôt dráhy bola zrejme zmeraná zle a aká mala byť jej skutočná hodnota.
Najviac sa od seba líšia rýchlosť od 6. do 9. sekundy (7,3 cm / s) a od 9. do 12. sekundy (14 cm / s) ⇒ hodnota dráhy v 9 sekunde je zrejme zle zmeraná a mala by byť väčšia (tým sa prvá rýchlosť zväčší a druhá zmenší).
Pedagogická poznámka: Najľahšie sa žiakmi navrhovaná hodnota otestuje, ak máte dáta v tabuľkovom procesore. Môžete pokusne meniť a sledovať, ako sa menia hodnoty rýchlosťou.
Dá sa tak nájsť aj „ideálny“ hodnota dráhy, pri ktorej vychádza pohyb najrovnomernejšie.

Pr. 7: Nájdi vlastnosť, podľa ktorej je možné rozoznať rovnomerný pohyb už z hodnôt dráhy bez počítania rýchlosťou. Ak je pohyb rovnomerný, musí sa dráha rovnomerne zväčšovať ⇒ ak je tabuľka
nameraná so stálym časovým intervalom, musí sa dráha rovnomerne zvěšovat = rozdiely medzi jednotlivými hodnotami dráhy sú približne rovnaké.
Pr. 8: Ako bude vyzerať graf závislosti dráhy vozíka na čase? Ako bude vyzerať graf závislosti rýchlosti na čase? Zakreslite obaja odhady do jedného obrázku.
Graf dráhy: Urazená dráha sa stále rovnako zväčšuje ⇒ grafom dráhy bude približne šikmá stúpajúca čiara.
Graf rýchlosti: Okamžitá rýchlosť je stále rovnaká ⇒ grafom rýchlosti bude vodorovná čiara.

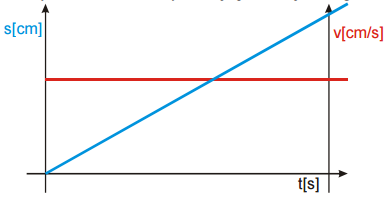
Pr. 9: Nakresli na milimetrový papier do jedného grafu závislosť dráhy na čase (os na ľavej strane) a závislosť rýchlosť na čase (os na pravej strane). Pred nanášaním hodnôt si rozmysli všetky merítka tak, aby si čo najlepšie využil plochu grafu. Čím sa vyznačuje
graf závislosti dráhy rovnomerného pohybu na čase? Čím sa vyznačuje graf rýchlosti rovnomerného pohybu na čase?
Mierka:
• čas (vodorovná os): 18 dielikov, 9 hodnôt času po 3 sekundách ⇒ dva dieliky zodpovedajú 3 sekundám,
• dráha (zvislá os): 14 dielikov, hodnoty do 278 cm ⇒ 1 dielik zodpovedá 20 cm,
• rýchlosť (zvislá os): 14 dielikov, hodnoty do 11,3 cm / s ⇒ 1 dielik zodpovedá 1 cm / s.
Grafom dráhy rovnomerného pohybu je približne priamka
Grafom rýchlosti rovnomerného priehybu je približne vodorovná priamka.
Zhrnutie: Pri meraní rovnomerného pohybu nenameriame kvôli rôznym chybám ideálne hodnoty a nemôžeme tak očakávať, že pre všetky intervaly získame presne rovnaké hodnoty rýchlosti.

Pr. 1: Pozri si obrázok. Kto a čo je z hľadiska výpravcu v pokoji? Čo sa naopak z hľadiska výpravcu pohybuje? Vidí cestujúci vo vlaku to isté? Ako vidí situáciu dieťa, ktoré sa točí na kolotoči?
Pr. 2: Popíš, za akej situácie sa môže dôjsť k nasledujúcemu pozorovanie.
a) Vodič idúceho auta vidí, že vlak voči nemu stojí.
b) Cestujúci v idúcom vlaku stojí voči stanici.

Na obrázku je zakreslené, ako išlo auto. Dokresli do obrázka po akej dráhe sa pohybuje: a) vlak b) sedačka kolotoča c) pes d) cyklista.
Pr. 3: Kto alebo čo sa na obrázku pohybuje: a) priamočiarym pohybom;
b) křivočarým pohybom; c) pohybom po kružnici.
Pr. 4: Nakresli obrázok rieky (zvrchu). Akým smerom musíme veslovať na lodi, aby sme sa dostali priamo na protiľahlý breh?
Pr. 5: Na papieriku je krížikom vyznačený bod. Akými číslami je popísaná jeho poloha?

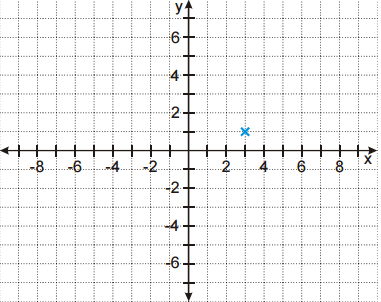
Pr. 6: Dokresli do obrázka body o súradniciach: B [5; 2]; C [0; 3]; D [-2; 4]; E [-6; 0].
Pr. 7: Pomocou súradníc sa dá popisovať nielen poloha bodov na papieri, ale aj poloha predmetov v priestore (napríklad v triede). Vystačíme s dvoma súradnicami ako pri určovanie polohy v rovine? Čo všetko musíme dohodnúť, aby sme si pod rovnakými súradnicami predstavili rovnaký bod v triede?
Pr. 8: Popíš pomocou súradníc polohu nasledujúcich predmetov v triede. Trieda je vysoká 4 m, dlhá 8 m a široká 6,5 m. Počiatok sústavy súradníc leží v dolnom prednom roka učebne pri okne, os x smeruje po zemi pozdĺž okien k zadnej stene, os y pozdĺž
predné steny k dverám a os z ide kolmo hore. Urči súradnice nasledujúcich bodov:
a) vodovodný kohútik na katedre, b) ľavý predný roh prvej lavice pri okne,
c) hodiny, d) ľavý (z pohľadu triedy) reproduktor.
Pr. 9: Ktoré predmety sú v triede určené nasledujúcimi súradnicami.
a) [0; 0; 3,5] b) [0; 4; 2] c) [7; 5,5; 1] d) [5; 1; 1]

Pomôcky: papieriky s obrázkami
Poznámka: Obrázky sú prevzaté z učebnice „Fyzika okolo nás“ so súhlasom vedúceho autorského kolektívu Doc. Milana Rojko. Ak by niekto považoval ich prevzatie za porušenie autorských práv, po upozornení je ihneď stiahneme.

Pr. 1: Pozri si obrázok. Kto a čo je z hľadiska výpravcu v pokoji? Čo sa naopak z hľadiska výpravcu pohybuje? Vidí cestujúci vo vlaku to isté? Ako vidí situáciu dieťa, ktoré sa točí na kolotoči?
Pohľad výpravcu:
• v pokoji: stromy, budova stanice, auto pri prejazde, okolité kopce, značky a pätníky okolo cesty, stolička pri vode, …
• v pohybe: vlak a cestujúci vo vnútri, deti na kolotoči, otáčavá časť kolotoče, chlapec na skateboarde, pes, prievozník na lodičke, lietadlo, …
Cestujú vo vlaku nevidí to samo. Zdá sa im, že všetko, čo je voči výpravcovi v pokoji sa voči vlaku pohybuje, naopak všetkých predmety vo vlaku sú voči nim v pokoji. Deti na kolotoči vidí opäť niečo iné – všetko sa okolo nich zložito otáča.

Pr. 2: Popíš, za akej situácie sa môže dôjsť k nasledujúcemu pozorovanie.
a) Vodič idúceho auta vidí, že vlak voči nemu stojí.
b) Cestujúci v idúcom vlaku stojí voči stanici.
a) Vodič idúceho auta vidí, že vlak voči nemu stojí.
Cesty aj železničná trať vedú priamo vedľa seba a auto aj vlak idú rovnakou rýchlosťou vedľa seba ⇒ ich vzájomná poloha sa potom nemení a pozorujú, že sa voči sebe nepohybujú.
b) Cestujúci v idúcom vlaku stojí voči stanici.
Ak vlak ide pomaly a cestujúci ide (beží) rovnakou rýchlosťou proti smeru jazdy, voči nádražie sa nepohybuje.
Keď hovoríme o pohybe (pokoja), musíme vždy udať, odkiaľ sa pozeráme ⇒ pohyb i kľud je relatívna.

Pr. 3: Na obrázku je zakreslené, ako išlo auto. Dokresli do obrázka po akej dráhe sa pohybuje: a) vlak b) sedačka kolotoča c) pes d) cyklista.

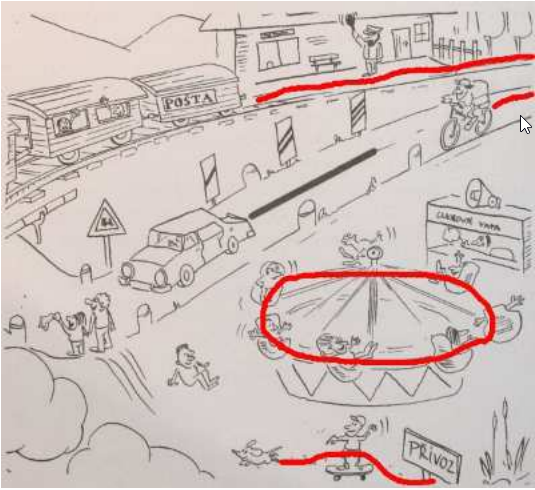
Pr. 4: Kto alebo čo sa na obrázku pohybuje: a) priamočiarym pohybom;
b) křivočarým pohybom; c) pohybom po kružnici.
a) priamočiarym pohybom sa pohybovalo auto, cyklista na ceste a lietadlo.
b) Křivočarým pohybom sa pohybuje pes, vlak, ruka výpravcu s plácačkou, vreckovku v ruke dieťaťa.
c) Pohybom po kružnici sa pohybujú deti na kolotoči, kolesá pri vlaku.

Pr. 5: Nakresli obrázok rieky (zvrchu). Akým smerom musíme veslovať na lodi, aby sme sa dostali priamo na protiľahlý breh?
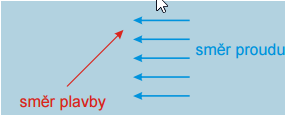Musíme sa pohybovať šikmo proti prúdu tak, aby sme vyšli proti prúdu rovnakú vzdialenosť, o akú nás prúd znesie.
Pedagogická poznámka: Bývaly doby, kedy som okolo zavádzania sústavy súradníc robil veľa okolkov (hra na lode, …). Tento rok ukázal, že je zrejme to zbytočné. Časť žiakov o súradniciach určite počula, ale aj ten zvyšok sa bez rozpakov shodnul na riešenie nasledujúceho
príkladu a so súradnicami začal ihneď pracovať.
Pr. 6: Na papieriku je krížikom vyznačený bod. Akými číslami je popísaná jeho poloha?

Poloha krížika môže byť popísaná dvoma spôsobmi:
• 3; 1
• 1; 3
Záleží na tom, ktoré z čísel napíšeme ako prvý ⇒ dohoda: ako prvé píšeme číslo, ktoré udáva polohu v smere osi x (vo vodorovnom smere). Aby bolo hneď jasné, že čísla znamenajú polohu bodu, píšeme ich do hranatých zátvoriek: [3; 1].
Polohu bodu v rovine určujeme pomocou dvoch čísel (súradníc), ktoré píšeme do hranatých zátvoriek [x y; ]. Ako prvý vždy píšeme hodnotu x-ovej súradnice.
Priamky x a y označujeme ako osi sústavy súradníc, ich priesečník ako počiatok sústavy súradníc.
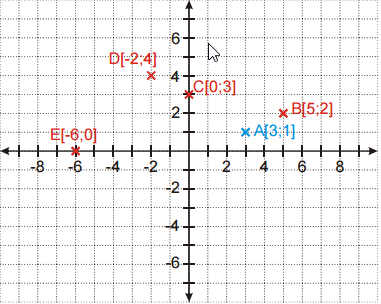
Pr. 7: Dokresli do obrázka body o súradniciach: B [5; 2]; C [0; 3]; D [-2; 4]; E [-6; 0].

Pr. 8: Pomocou súradníc sa dá popisovať nielen poloha bodov na papieri, ale aj poloha predmetov v priestore (napríklad v triede). Vystačíme s dvoma súradnicami ako pri
určovanie polohy v rovine? Čo všetko musíme dohodnúť, aby sme si pod rovnakými súradnicami predstavili rovnaký bod v triede?
V priestore budeme potrebovať tri súradnice (dĺžku, šírku, výšku).
Musíme dohovoriť:
• miesto, v ktorom sa všetky osi budú pretínať (počiatok sústavy súradníc),
• smery všetkých troch osí.
Pr. 9: Popíš pomocou súradníc polohu nasledujúcich predmetov v triede. Trieda je vysoká
4 m, dlhá 8 m a široká 6,5 m. Počiatok sústavy súradníc leží v dolnom prednom roka učebne pri okne, os x smeruje po zemi pozdĺž okien k zadnej stene, os y pozdĺž predné steny k dverám a os z ide kolmo hore.

Urči súradnice nasledujúcich bodov:
a) vodovodný kohútik na katedre, b) ľavý predný roh prvej lavice pri okne,
c) hodiny, d) ľavý (z pohľadu triedy) reproduktor.
a) vodovodný kohútik na katedre: [1; 4; 1, 2],
b) ľavý predný roh prvej lavice u okna: [2,5; 1; 0,6],
c) hodiny: [2,5; 6,5; 2,5],
d) ľavý (z pohľadu triedy) reproduktor [0; 2; 3].
Pr. 10: Ktoré predmety sú v triede určené nasledujúcimi súradnicami.
a) [0; 0; 3,5] b) [0; 4; 2] c) [7; 5,5; 1] d) [5; 1; 1]
a) [0; 0; 3,5]: predný horný roh triedy pri okne.
b) [0; 4; 2]: pravý horný roh tabule.
c) [7; 5,5; 1]: pravý roh poslednej lavice pri dverách.
d) [5; 1; 1]: pravý horný roh katedry, bližšie pri stene.
Zhrnutie: Pohyb je relatívna – záleží na pozorovateľovi.