Pr. 1: Preveď na jednotky v zátvorke.
a) 5 m  [cm] b) 1200 mm [cm] c) 6 km [m]
d) 50 m [dm] e) 17 m  [mm] f) 30 dm [mm]
g) 6 cm [mm] h) 4000 dm [m] i) 15 km dm []
Pr. 2: Prečo sme pri meraní 30 cm pravítkom nezískali rovnako presný výsledok ako s milimetrovým pásmom?
Pr. 3: Doplň tabuľku s nameranými hodnotami šírky katedry o posledný stĺpec s rozmedzím, v ktorom leží skutočná hodnota. Zodpovedajú presnejšie namerané hodnoty rozmedzím menej presných meraní? typ merania nameraná hodnota hodnota leží v rozmedzí

Pr. 4: Pozri si v učebnici na strane 23 fotografie rôznych meradiel. Ktoré z nich poznáš a používal si je pri meraní? Ktoré z nich umožňuje merať vzdialenosti s najväčšou presnosťou? Čím za túto presnosť merania „platíme“ (akú nevýhodu táto presná meradla majú)?
Pr. 5: Odhadni vyznačenej veľkosti nasledujúcich predmetov:
a) dĺžka huby na tabuľu, b) šírka triedy,
c) hrúbka kriedy, d) výška krabičky,
e) hrúbka dosiek zošita.
Vyber pre každú z veľkostí zodpovedajúcej meradlo a odhady skontroluj meraním.
Pr. 6: Zmeraj pravítkom šírku lavice. Porovnaj presnosť svojho výsledku s presnosťou merania pomocou murárskeho metra.

Pr. 7: spočítame priemer z hodnôt, ktoré si nameral sa spolužiakmi v jednej lavici a porovnaj ho s hodnotou nameranou metrom.
Pr. 8: Má zmysel merať rozmery miestnosti na mm? Prečo?
Pr. 9: S akou presnosťou sa meria vzdialenosti medzi mestami? S akou presnosťou sa stavia domy?
S akou sa vyrába nábytok? S akou sa rozmerom záhony na záhrade? S akou sa vyrubujú pozemky? S akou presnosťou sa obrába v súčiastky do strojov?
Pr. 10: Zmeraj pravítkom hrúbku listov v učebnici.
Pr. 11: Nájdi postup, ako zmerať pravítkom obvod PET fľaše.
Pr. 12: 1 meter bol najskôr stanovený ako desetimilióntina zemského kvadrantu (zemský kvadrant je vzdialenosť pólu od rovníka). Vysvetli, prečo je dĺžka rovníka (obvod zemegule) veľmi blízka hodnote 40 000 km.
Domáce bádania: (povinne) Zmeraj dĺžku Tvoje cesty domov. Ak jazdíš autobusom alebo vlakom zmeraj dĺžku cesty zo školy na zastávku alebo zo zastávky domov. Ak ťa vozia autom alebo jazdíš na bicykli, zvoľ časť cesty, ktorú je možné ujsť pešo za menej ako štvrť hodiny.
Priebeh merania a výsledok zapíš a porovnaj s výsledkami merania pomocou jedného z internetových serverov (www.mapy.cz, www.google.com, …).
Domáce bádania: Zisti, akým spôsobom meria prejdenú vzdialenosť cyklopočítač. akým trikom by bolo možné zariadiť, aby meral väčšiu vzdialenosť a väčšiu rýchlosť, než skutočne ujedeš?
Domáce bádania: Navrhni spôsob, ako zmerať čo najpresnejšie výšku školy.

Pomôcky: meter, zavinovacie meter, krajčírsky meter, Šuplera, metrický skrutku, pásmo, povrázok s vyznačeným metrom, špagát s vyznačenými decimetre, pravítko 30 cm
Pedagogická poznámka: Žiaci prevádzajú a počas tejto doby nechávam vybrané dvojice premerať rôznymi meradlami šírku katedry.
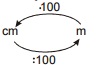
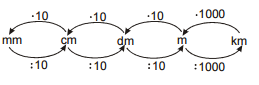
Pr. 1: Preveď na jednotky v zátvorke.
a) 5m [cm] b) 1200 mm [cm] c) 6km [m]
d) 50 m  [dm] e) 17 m [mm] f) 30dm  [mm]
g) 6cm [mm] h) 4000dm [m] i) 15km  [dm]
a) 5 m = 500 cm b) 1200 mm = 120 cm  c) 6 km = 6000m
d) 50 m = 500dm  e) 17 m = 17 000 mm  f) 30 dm = 3000 mm
g) 6 cm = 60 mm  h) 4000 dm = 400 m  i) 15 km = 150000dm
Pedagogická poznámka: Nadpis posledného stĺpca na tabuli napíšem samozrejme až neskôr.
Šírka katedry meraná rôznymi spôsobmi (výsledky zapisuj do tabuľky) typ merania nameraná hodnota odhad na metre 1 m
špagát s vyznačenými decimetre 8,9 dm centimetrová tyč 90 cm
pravítko 30 cm 89 cm pásmo s milimetrovou stupnicou 89,8 cm
Ako je možné, že sme nezískali rovnaké hodnoty? Ktorá z hodnôt je správna?
Úplne správna nie je ani jedna, nie je možné merať úplne presne, vždy meriame s určitou nepresností, ktorá súvisí s použitým meradlom.
Ak odhadneme šírku stola na 1 m s presnosťou 1m, znamená to, že jeho skutočná dĺžka l leží medzi číslami 0,5 m až 1,5 m (0,5m < / <1,5m ) – polovica dielika na obe strany.
Ak sa nám podarí šírku stola zmerať s väčšou presnosťou, mal by presnejší údaj ležať v rozmedzí, ktoré sme získali pri predchádzajúcom pokuse.
Pedagogická poznámka: Časť žiakov sa ťažko zmieruje s tým, že by katedra nemala šírku 90 cm ( „Prečo by vyrábali pracovnú dosku širokou 89,8 cm?“). V danom mieste má katedra
naozaj 89,8 cm. Dôvodov môže byť viac – doska nie je presná, materiál reaguje na vzdušnú vlhkosť (alebo sa naopak seschnul), samotná drevotrieska je užší, pretože sa na nej ešte lepší
povrchová fólia, ktorá j tenšie než sa čakalo (alebo viac zažehlené), …

Pr. 2: Prečo sme pri meraní 30 cm pravítkom nezískali rovnako presný výsledok ako s milimetrovým pásmom?
Pravítko bolo príliš krátke, museli sme ho posúvať a zrejme sme pri tom neboli dostatočne presní.
Pr. 3: Doplň tabuľku s nameranými hodnotami šírky katedry o posledný stĺpec s rozmedzím, v ktorom leží skutočná hodnota. Zodpovedajú presnejšie namerané hodnoty rozmedzím menej presných meraní?

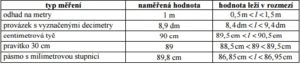
Presnejšie merania zodpovedajú rozmedzím z predchádzajúcich meraní. Jedinou výnimkou je 30 cm pravítko, kde sme urobili chybu pri posunovaní pravítka.
Pr. 4: Pozri si v učebnici na strane 23 fotografie rôznych meradiel. Ktoré z nich poznáš a používal si je pri meraní? Ktoré z nich umožňuje merať vzdialenosti s najväčšou presnosťou? Čím za túto presnosť merania „platíme“ (akú nevýhodu táto presná
meradla majú)?
Najväčší presnosť merania umožňuje posuvné meradlo a mikrometer. Ich nevýhodou je skutočnosť, že umožňujú merať len malej vzdialenosti (do 20 cm).
Pedagogická poznámka: Žiaci poznajú rôzne druhy metrov, ale napríklad Šupler ich videlo len niekoľko a samotné označenie Šuplera nepoznal nikto.
Pr. 5: Odhadni vyznačenej veľkosti nasledujúcich predmetov:
a) dĺžka huby na tabuľu, b) šírka triedy,
c) hrúbka kriedy, d) výška krabičky,
e) hrúbka dosiek zošita.
Vyber pre každú z veľkostí zodpovedajúcej meradlo a odhady skontroluj meraním.
a) dĺžka huby na tabuli
Pravítko, murársky meter: 20 cm.
b) šírka triedy
Pásmo: 6,42 m
c) hrúbka kriedy
Posuvné meradlo, mikrometrický skrutka: 11,8 mm.
d) výška škatuľky
Pravítko, posuvné meradlo: 2,7 cm.
e) hrúbka dosiek zošita.
Mikrometrický skrutka: 0,35 mm.

Pedagogická poznámka: Meradlá vyberajú žiaci z hromady na stole, meranie vykonávam ja.
Neučíme sa merať Šupler ani mikrometrickou skrutkou (látka prvého ročníka). keď som mikrometrický skrutku používal, žiakmi veľmi zaujalo, že ničím neposúva, ale otáčam, ako by nemali žiadnu skúsenosť s posunom po skrutkovici (napríklad od skrutkovanie).
Pr. 6: Zmeraj pravítkom šírku lavice. Porovnaj presnosť svojho výsledku s presnosťou merania pomocou murárskeho metra.
Pravítko (je kratší ako lavica ⇒ merania je ťažké): 43,5 cm.
Murársky meter: 43 cm.
Presnejšie je zrejme meranie murárskym metrom (meriame lavicu naraz).
Pedagogická poznámka: Objavujú sa aj názory, že presnejšie je meranie pravítkom, pretože meter môže byť trochu nakrivo.
Rozdiely v oboch meraní bývajú len u niektorých žiakov, Ti obozretnejšie väčšinou zmeria oboma spôsobmi to isté.
Pedagogická poznámka: Metre deťom rozdávam do lavíc s tým, že až dôjdem na koniec triedy, začnem je od začiatku opäť vyberať. Inak sa meranie preťahuje na niekoľkonásobok, pretože
meter je jednou z najlepších hračiek.
Prečo pravítkom nemeriame rovnako presne ako metrom?
Pravítko je kratšia ako lavica ⇒ musíme ho nastavovať a pri tom robíme chyby (rovnako ako pri merania katedry).
Je možné zmerať lavicu spoľahlivejšie, aj keď budeme mať k dispozícii len pravítko?
Pri meraní pravítkom môžeme urobiť chybu na obe strany (namerať viac aj menej než aká je skutočnosť) ⇒ merania zopakujeme viackrát a spočítame priemer.
Pr. 7: spočítame priemer z hodnôt, ktoré si nameral sa spolužiakmi v jednej lavici a porovnaj ho s
hodnotou nameranou metrom.
Ďalšie merania: 43,3 cm, 42,8 cm.
Priemer:

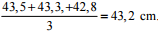
Priemerný výsledok je bližšie k presnejšiemu meranie.
Pedagogická poznámka: Výpočet priemeru je vďaka slovenskej posadnutosti známkami asi jedinou zručností, ktorú môžete predpokladať u každého žiaka.
Vypočítaný priemer je väčšinou bližšie k hodnote nameranej metrom, u jednotlivca však nemáte žiadnu istotu, že meranie takto dopadne. Dôležité je aj to, aby pravítkom merali ešte pred tým než získajú správnu hodnotu pomocou murárskeho metra.
Pr. 8: Má zmysel merať rozmery miestnosti na mm? Prečo?
Nemá, na rôznych miestach by sme získali rôzne hodnoty.

Pr. 9: S akou presnosťou sa meria vzdialenosti medzi mestami? S akou presnosťou sa stavia domy?
S akou sa vyrába nábytok? S akou sa rozmerom záhony na záhrade? S akou sa vyrubujú pozemky? S akou presnosťou sa obrába v súčiastky do strojov?
Vzdialenosti medzi mestami – km,
stavba domov: cm,
nábytok: mm
záhony na záhrade: dm, cm
vymeranie pozemkov: m, dm,
súčiastky do strojů: mm, desatiny aj stotiny mm.
Pr. 10: Zmeraj pravítkom hrúbku listov v učebnici.
Hrúbka listov v učebnici je príliš malá na meranie pravítkom.
Trik: zmeriame hrúbku všetkých listov v učebnici a vydelíme získanú vzdialenosť počtom listov.
Hrúbka učebnice bez dosiek: 6 mm.
Počet listov: 120: 2 60 = (počet strán: 2, pretože každý list má dve strany).
Hrúbka jedného listu: 6: 60 0,1 = mm.
List v učebnici má hrúbku približne 0,1 mm.
Pr. 11: Nájdi postup, ako zmerať pravítkom obvod PET fľaše.
Problém: pravítko je rovné a nejde ohnúť okolo fľaše.
Ovinieme fľašu papierikom, označíme si špendlíkom dva body.

Vzdialenosť vyznačených bodov potom premeriame.

obvod PET fľaše je 20,5 cm.
Pr. 12: 1 meter bol najskôr stanovený ako desetimilióntina zemského kvadrantu (zemský
kvadrant je vzdialenosť pólu od rovníka). Vysvetli, prečo je dĺžka rovníka (obvod zemegule) veľmi blízka hodnote 40 000 km.
Vzdialenosť od pólu k rovníku je desať miliónov metrov 10 000 000 m = 10 000 km a je štvrtinou obvodu Krajina ⇒ obvod Zeme (a teda i rovník) meria 40 000 km.
Domáce bádania: (povinne) Zmeraj dĺžku Tvoje cesty domov. Ak jazdíš autobusom alebo vlakom zmeraj dĺžku cesty zo školy na zastávku alebo zo zastávky domov. Ak ťa vozia autom alebo jazdíš na bicykli, zvoľ časť cesty, ktorú je možné ujsť pešo za menej ako štvrť hodiny.
Priebeh merania a výsledok zapíš a porovnaj s výsledkami merania pomocou jedného z internetových serverov (www.mapy.cz, www.google.com, …).
Domáce bádania: Zisti, akým spôsobom meria prejdenú vzdialenosť cyklopočítač. akým trikom by bolo možné zariadiť, aby meral väčšiu vzdialenosť a väčšiu rýchlosť, než skutočne ujedeš?
Domáce bádania: Navrhni spôsob, ako zmerať čo najpresnejšie výšku školy.
Zhrnutie: Vždy meriame s chybou.

Pr. 1: Na čom sa rybári musia dohodnúť, aby mohli súťažiť o najväčšiu chytenú šťuku?
Pr. 2: Zo sveta zmizla všetky pravítka, trojuholníky a iné meradlá. Zmeraj bez nich šírku lavice. Výsledky svojho merania zapíš do zošita tak, aby podľa Tvojho merania mohol ktokoľvek nakresliť šírku lavice na tabuľu.
Pr. 3: Merať je možné aj úplne bez pomôcok. Ak prídeš na to ako, zmeraj šírku triedy. aké nevýhody a aké výhody má tento spôsob merania?
Pr. 4: Čo je podstatou všetkých predchádzajúcich meraní?
Pr. 5: Vypíš v súčasnosti používané jednotky dĺžky. Ku každej jednotke uveď príklady vzdialeností, ktoré je vhodné v nej merať.
Pr. 6: Preveď na metre.
a) 12 km b) 3500cm c) 120000 mm
d) 300dm e) 200 km c) 50000 mm
Pr. 7: Preveď na jednotky v zátvorke.
a) 12 m  [cm] b) 3500 mm  [dm] c) 12 km  [m]
d) 35m  [dm] e) 3m  [mm] f) 120dm  [mm]
g) 350cm  [mm] h) 800dm  [m] i) 3km  [cm]
mm Na obrázku sú znázornené prevodné vzťahy medzi metrom a centimetrom. Pokiaľ prevádzame z metrov na centimetre (šípka od m k cm), násobíme hodnotu stem (⋅100). Ak prevádzame z centimetrov na metre (šípka od cm k m), delíme stem (: 100).

Vypiše do radu známej jednotky dĺžky od najmenšej k najväčšej a list k nim prevodné vzťahy medzi susednými jednotkami.
Pr. 9: Svetlo sa vo vákuu (takmer prázdny priestor medzi planétami a hviezdami) pohybuje obrovskou rýchlosťou – každú sekundu uletí 300 000 km. Vzdialenosť, ktorú svetla vo vákuu uletí, používajú astronómovia na udávanie vzdialeností (ktoré sú vo vesmíre nepredstaviteľne obrovské). Napríklad Zem je od Mesiaca vzdialená 1 svetelnú sekundu, od Slnka 8 svetelných minút a od najbližšej hviezdy 4 svetelné roky. preveď
tieto vzdialenosti na km.
Domáce bádania: Odhadni rozmery desiatich rôznych predmetov vo svojom okolí. odhadnuté rozmery potom premerajte zodpovedajúcim meradlom (pravítko, zvinovací meter, krajčírsky
meter). Odhad aj výsledok merania zapíš do zošita.

Domáce bádania: V anglosaských krajinách (USA, Anglicko) sa ešte stále používajú anglosaskej jednotky dĺžky: palec (inch), stopa (foot), yard a míle. Nájdi prevodné vzťahy medzi týmito
jednotkami a preveď 2 míle na ostatné jednotky. Aká je výhoda prevádzanie v metrickom systému?

Pomôcky: čierna skrinka (2 kusy)
Večný problém rybárov: „Chytil som tááákovouhle rybu“. Ako zabezpečiť, aby si všetci mohli verne predstaviť, akú rybu som chytil?
Pr. 1: Na čom sa rybári musia dohodnúť, aby mohli súťažiť o najväčšiu chytenú šťuku?
Rybári sa musia dohodnúť na dvoch veciach:
• čo presne si predstavujú pod pojmom dĺžka ryby (napríklad od špičky hlavy ku koncu chvostovej plutvy),
• akú jednotku budú k meranie používať (napríklad metre).
Pr. 2: Zo sveta zmizla všetky pravítka, trojuholníky a iné meradlá. Zmeraj bez nich šírku lavice. Výsledky svojho merania zapíš do zošita tak, aby podľa Tvojho merania mohol ktokoľvek nakresliť šírku lavice na tabuľu.
Príklady z našej triedy: 3 piade, dva zošity A4 na šírku, jeden a pol zošita A4 na výšku, štyri pastelky, ……
Pedagogická poznámka: Pri kontrole realizujem dĺžky na tabuľu. Je tak vidieť, že potrebujem predmet, ktorý žiaci používali na meranie a že pri použití častí tela dostávame rôzne
výsledky.
Pr. 3: Merať je možné aj úplne bez pomôcok. Ak prídeš na to ako, zmeraj šírku triedy. aké nevýhody a aké výhody má tento spôsob merania?
Merať môžeme pomocou časťou svojho tela: šírka triedy na napríklad 25 stôp, 22 stôp, 8 krokov, 6 krokov.
Výhody: meradlo máme neustále po ruke.
Nevýhody: Každému to meria inak.
Pr. 4: Čo je podstatou všetkých predchádzajúcich meraní?
Pri meraní porovnávame, koľkokrát sa na danej veci zopakuje meracia jednotka (koľkokrát je táto vec väčšie).
Pedagogická poznámka: Krokovanie triedy je pre vizualizáciu tejto myšlienky veľmi vhodné.
Preto sa pýtam žiakov, čo robili, keď merali triedu.
Pri meraní porovnávame, koľkokrát sa na danej veci zopakuje meracia jednotka
Na meranie potrebujeme:
• vyjasniť, čo si vlastne meriame (veličina),
• vzdialenosť, pomocou ktorej dĺžku vyjadríme (jednotka).
Nevýhody merania pomocou bežných vecí: Každá ceruzka, každý peračník je trochu iný.
Meranie pomocou častí tela:
• Výhody: meradlo máme stále po ruke, ľahko si dokážeme jednotku predstaviť.
• Nevýhody: každý je trochu inak veľký a tak máme všetci inej jednotky.
Vladári sa snažili jednotky zjednocovať, ale každý štát meral trochu inak.

1789 – Veľká francúzska revolúcia:

Všetko sa zmenilo (vrátane názvov mesiacov a dní) ⇒ dobrá príležitosť zmeniť aj jednotky ⇒ metrický systém. Pôvodne platil len vo Francúzsku, postupne ho prebrali aj ďalšie krajiny (dnes ho oficiálne nepoužívajú iba tri štáty – USA, Barma a Libéria). Systém sa postupne vyvíjal, súčasná variant SI bola zavedená v roku 1960.
Základnou jednotkou dĺžky je 1 meter (skratka 1 m).
Ako sa zdokonaľovali metódy merania, pôvodné definície jednotiek bolo nutné meniť. Napríklad definícia metra sa vylepšovala takto:
• 1793: 1 meter je desetimilióntina zemského kvadrantu (zemský kvadrant je vzdialenosť pólu od rovníka).
• 1889: 1 meter je vzdialenosť rysiek na medzinárodnom prototypu metra uloženom v ústave pre miery a váhy v Serves pri Paríži.
• 1960: 1 meter je rovný 1,650,763.73 vlnových dĺžok oranžovej emisné čiary atómu kryptónu 86 meranej vo vákuu.
• 1983: 1 meter je dĺžka, ktorú prejde svetlo vo vákuu za 1s
299 792 458.
Dodatok: Je zaujímavé, že názvy dní a mesiacov, ktoré boli pri francúzskej revolúcii zavedené, sa neujali. Zato nové jednotky sa presadili (s výnimkou jednotiek času, kde bola ľudská zotrvačnosť silnejší), pretože prinášali podstatné zjednodušenie.
Pedagogická poznámka: Keď je čas, rozprávame sa tom, ako ťažké je zmeniť jednotky. Aby sme neustále nepísali, používame namiesto názvov veličín značky:
• dĺžka … l, d
• šírka … s
• výška … v, h
• hĺbka … h
• priemer … d
• polomer … r
Nie vždy je značenie dodržiavané, najlepším vodidlom tak zostáva porozumenie konkrétny situáciu.
Vyjadrovať všetky dĺžky iba v metroch by bolo nepohodlné (niekedy by hodnoty boli zbytočne malé, inokedy zbytočne veľké) ⇒ okrem základnej jednotky 1 meter sa používajú aj jednotky odvodené pomocou predpôn. Každá predpona predstavuje vždy rovnaký násobok alebo diel základnej jednotky (napríklad predpona kilo znamená 1000 násobok). Tým sa radikálne zjednodušilo prevádzanie, ktoré bolo predtým veľmi nepohodlné.

Dodatok: Konvertovanie jednotiek napríklad v klasickom anglosaskom systéme, ktorý sa dodnes používa v USA je ďaleko zložitejšie (napríklad 1 míľa, ktorá hrá úlohu kilometra, má 1760 yardov, ktoré hrajú úlohu metrov). Potom napríklad 0,3 míle predstavuje 0,3 * 1760 528 = yardov.
Pr. 5: Vypíš v súčasnosti používané jednotky dĺžky. Ku každej jednotke uveď príklady vzdialeností, ktoré je vhodné v nej merať.
kilometer (km) – vzdialenosť medzi mestami,
meter (m) – výška budov, rozmery miestností
decimeter (dm) – rozmery látky,
centimeter (cm) – výška postavy, rozmery obrázkov v zošite
milimeter (mm) – presné rysovanie, rozmery pri výrobe nábytku
Pr. 6: Preveď na metre.
a) 12 km b) 3500C c) 120000 mm
d) 300D e) 200 km c) 50000 mm
a) 12 km = 12000m = b) 3500C = 35m
c) 120000 mm = 120 m d) 300dm = 30 m
e) 200 km = 200000 f) 50000mm = 50 m
Pr. 7: Preveď na jednotky v zátvorke.
a) 12 m  [cm] b) 3500 mm  [dm] c) 12 km  [m]
d) 35m  [dm] e) 3m  [mm] f) 120dm  [mm]
g) 350cm  [mm] h) 800dm  [m] i) 3km  [cm]
a) 12 m = 1200 cm b) 3500mm = 35dm  c) 12 km = 12000m
d) 35m = 350dm  e) 3m = 3000mm  f) 120dm = 12000 mm
g) 350cm = 3500 mm  h) 800dm = 80 m  i) 3km = 300000cm
Pr. 8: Na obrázku sú znázornené prevodné vzťahy medzi metrom a centimetrom. Pokiaľ prevádzame z metrov na centimetre (šípka od m k cm), násobíme hodnotu stem (:100).
Ak prevádzame z centimetrov na metre (šípka od cm k m), delíme stem (:100).

Vypiše do radu známej jednotky dĺžky od najmenšej k najväčšej a list k nim prevodné vzťahy medzi susednými jednotkami.

Pedagogická poznámka: Schéma je zaradených až za prevody schválne. Žiaci ho na prevádzanie nepotrebujú (chyby, ktoré robia, väčšinou nepramení z toho, že by nepoznali pomery medzi jednotlivými jednotkami), dorobenie schéme je čiastočným cvičením zovšeobecňovania.
Pr. 9: Svetlo sa vo vákuu (takmer prázdny priestor medzi planétami a hviezdami) pohybuje obrovskou rýchlosťou – každú sekundu uletí 300 000 km. Vzdialenosť, ktorú svetla vo
vákuu uletí, používajú astronómovia na udávanie vzdialeností (ktoré sú vo vesmíre nepredstaviteľne obrovské). Napríklad Zem je od Mesiaca vzdialená 1 svetelnú sekundu, od Slnka 8 svetelných minút a od najbližšej hviezdy 4 svetelné roky. preveď tieto vzdialenosti na km.
• Mesiac (1 svetelná sekunda): za sekundu svetlo uletí 300 000 km ⇒ Mesiac je od Zeme
vzdialený 300 000 km.
• Slnko (8 svetelných minút): za 8 minút svetlo sekundu svetlo uletí
8 * 60 * 300000 = 144000000 km ⇒ Slnko je od Zeme vzdialené 144 000 000 km.
• Najbližšia hviezda (4 svetelné roky): za 4 roky svetlo uletí
4 * 365 * 24 * 60 * 60 * 300000 = 37 843 200 000 000 km ⇒ najbližšia hviezda je od Zeme vzdialená 37 843 200 000 000 km.
Žiaci prinesú nabudúce: učebnicu
Domáce bádania: Odhadni rozmery desiatich rôznych predmetov vo svojom okolí. odhadnuté rozmery potom premerajte zodpovedajúcim meradlom (pravítko, zvinovací meter, krajčírsky
meter). Odhad aj výsledok merania zapíš do zošita.
Domáce bádania: V anglosaských krajinách (USA, Anglicko) sa ešte stále používajú anglosaskej jednotky dĺžky: palec (inch), stopa (foot), yard a míle. Nájdi prevodné vzťahy medzi týmito
jednotkami a preveď 2 míle na ostatné jednotky. Aká je výhoda prevádzanie v metrickom systému?
Žiaci prinesú nabudúce: krajčírsky meter alebo iné meradlo bez milimetrové stupnice
Zhrnutie: Pri meraní si musíme ujasniť, čo meriame (veličinu) a pomocou čoho veľkosť vyjadrujeme (jednotku).