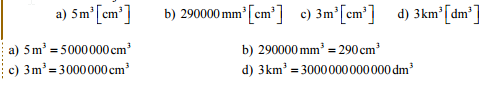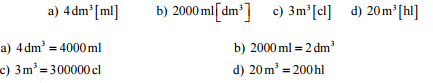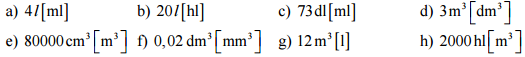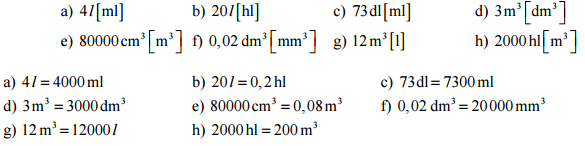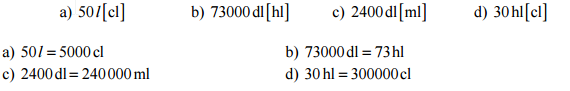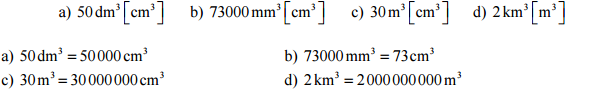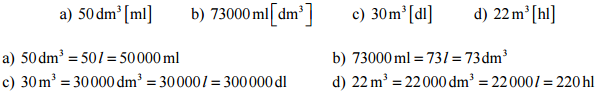Pr. 1: Preveď na jednotku v zátvorke.

Pr. 2: V ďalekej krajine menom Bezpředponie sa rozhodli uľahčiť život školskej mládeži a zrušili nielen všetky neštandardné jednotky ale aj všetky jednotkové predpony. Pre každú veličinu tak používali len základnú jednotku (pre dĺžku meter, pre čas sekundu). Za nedovolené používanie predpôn bol stanovený trest milión sekúnd väzenia, za používanie neštandardných jednotiek potom dokonca miliarda sekúnd väzenia. preveď
oba tresty na vhodné bežne používané jednotky.
Pr. 3: Akým číslom sa v Bezpřeponii udáva dĺžka jednej 45 minútovej vyučovacej hodiny? Na ako dlho odchádzania tunajší obyvatelia na týždennú dovolenku?
Pr. 4: Aké výhody a aké nevýhody má život v Bezpředponii?

Pomôcky: kyvadlo, stopky
Pedagogická poznámka: Konvertovanie v úvode hodiny nie je nutné. Ak sa doháňa kyvadlo z minulej hodiny, vynechávam ho.
Pr. 1: Preveď na jednotku v zátvorke.

Pedagogická poznámka: Nasledujúci časť hodiny samozrejme prebieha ako diskusia medzi deťmi. Kontrolu doby kyve úmyselne nechávam bokom, kvôli experimentálne kontrole vo škole. Deti si kyvadla prinesú z domu, prirábajú si ich na drôtený košík pod lavicou.
Často sa objavujú názory, že by perióda kyvadla mala závisieť na hmotnosti alebo počiatočný výchylke, vždy je rozoberáme, aby sme došli k tomu, že spomínaný efekt (potrebná väčšia
priťahovanie) síce existuje, ale je vyvážený iným efektom (väčšia zotrvačnosť). považujem to za dôležité, prirodzene žiaci uvažujú len jeden z efektov (ten, ktorý je napadol) a nesnažia sa
nájsť ďalšie (ktorý má tiež vplyv a mohol by vyrušiť ten prvý).
Čo sme zistili, pri výrobe kyvadla? Na čo musíme dať pozor? Na čom záleží, ako rýchlo sa kyvadlo kýva?
Záleží na dĺžke kyvadla (dĺžke povrázku). Dlhšie kyvadlo kýva pomalšie.
Nezáleží na:
• hmotnosti predmetu (ťažšie predmet si vo viacerých priťahuje Zeme, ale za sa s ním horšie
hýbe),
• veľkosť rozkývania (pri vyššej výchylke je kyvadlo viac naklonené a gravitácia ho viac urýchľuje, ale má pred sebou dlhšiu dráhu).
⇒ pri zostrojenie kyvadla nejde o nič iné než nájdenie správnej dĺžky.
Ako overíme, že kyvadlo už kýva správne?
Zmeranie jednej periódy nestačí, je veľmi nepresné ⇒ odmeriame dlhší časový úsek a spočítame, či kyvadlo urobí určený počet kmitov.
Pedagogická poznámka: Prvý návrh je väčšinou zmeranie jedného kmitu, keď s tým nie som spokojný, niekto s väčším počtom kmitov príde. V škole overujeme tak, že odštartujú
meranie a nechám deti počítať kmity. Po určitej dobe merania zastavím, nič nehovorím, deti nahlási, koľko napočítali a až na konci sám nahlásim, koľko sekúnd som meral (Naposledy sa počas 43 sekúnd počty kmitov líšili od 27 do 56). Na konci nechám žiakov do zošitov napísať, akú najdôležitejšie informáciu sme počas diskusie o Kyvadlo narazili
(Meranie viac period).
Pr. 2: V ďalekej krajine menom Bezpředponie sa rozhodli uľahčiť život školskej mládeži a zrušili nielen všetky neštandardné jednotky ale aj všetky jednotkové predpony. pre každú veličinu tak používali len základnú jednotku (pre dĺžku meter, pre čas sekundu). Za nedovolené používanie predpôn bol stanovený trest milión sekúnd väzenia, za používanie neštandardných jednotiek potom dokonca miliarda sekúnd väzenia. preveď
oba tresty na vhodné bežne používané jednotky.
Nejde o nič zvláštne, musíme previesť sekundy na väčšie jednotku (budeme prevádzať stále ďalej a zastavíme, až sa dostaneme k rozumnému číslu).

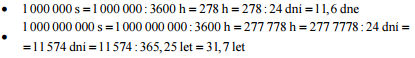
Za nedovolené používanie predpôn je trest 11,6 dní väzenia, za používanie neštandardných jednotiek 31,7 rokov.
Pr. 3: Akým číslom sa v Bezpřeponii udáva dĺžka jednej 45 minútovej vyučovacej hodiny?
Na ako dlho odchádzania tunajší obyvatelia na týždennú dovolenku?
Prevádzame na druhú stranu (na sekundy).
45 min = 45 * 60 s = 2700 s
1 týždeň = 7 dní * 24 h = 168 h = 168 * 3600 s = 604 800 s
Pr. 4: Aké výhody a aké nevýhody má život v Bezpriedponii?
Výhody:
• deti sa nemusia učiť predpony a nemusia sa učiť prevádzať,
• nemusí sa uvádzať jednotka (je jasná).
Nevýhody:
• hodnoty sú strašne veľké (alebo strašne malé),
• hodnoty sa zle predstavujú,
• vyplytvá sa veľa farby, …
Zhrnutie: Pri meraní opakujúcich sa dejov je výhodné merať dobu viac opakovaní.

Pr. 1: Na aké časti sa počítal čas pred vznikom civilizácie? Prečo? Čo majú všetky tieto časti spoločného?
Pr. 2: Dve z uvedených šiestich jednotiek nie sú považované za pravé fyzikálne jednotky. Ktoré to sú? Prečo?
Pr. 3: Zostav prevádzací schéma pre jednotky času (pravé fyzikálny).
Pr. 4: Preveď na jednotku v zátvorke.

Pr. 5: Nájdi princíp vystavených hodín: a) presýpacie hodiny, b) vodné hodiny, c) sviečkovej hodiny, d) slnečné hodiny
Pr. 6: Aké ďalšie druhy hodín poznáš?
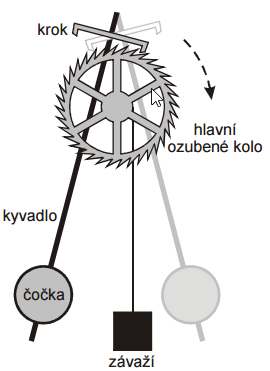
Pr. 7: Pomocou obrázku sa pokus vysvetliť, akým spôsobom riadi kyvadlo chod kyvadlových hodín.

Pr. 8: Preveď na jednotku v zátvorke.

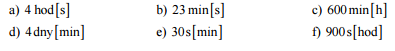
Domáce bádania: Chod kyvadlových hodín určuje kyvadlo. Zostroj kyvadlo z ťažkej matice (Alebo iného malého predmetu) zaveseného na tenkom povrázku. Od čoho závisí doba, po ktorou sa kyvadlo pohybu tam a späť (čas kmitu)? Zostroj kyvadlo ktorého doma kmitu je presne 1 s.

Pomôcky: vodné hodiny, presýpacie hodiny, sviečkovej hodiny, globus Jediná vec, ktoré nikto nemá dosť – čas.
Čas vnímame rôzne:
• keď je nuda, vlečie sa,
• keď sa niečo deje, PADI preč.
Človek nie je príliš dobrý prístroj na meranie času.
Pr. 1: Skús vysvetliť, prečo čas rýchlo uteká, keď robíme niečo, čo nás baví, a prečo sa vlečie, keď sa nudíme alebo musíme robiť niečo, čo nás nebaví. Keď robíme niečo, čo nás baví, nemyslíme na čas ⇒ nevníma, ako plynie a keď si ho konečne všimneme, tak máme pocit, že čas rýchlo ubehol.
Keď sa nudíme, môžeme na čas myslieť stále ⇒ jeho plynutie stále sledujeme a máme pocit, že sa strašne vlečie.
Pr. 2: Na aké časti sa počítal čas pred vznikom civilizácie? Prečo? Čo majú všetky tieto časti spoločného?
Deň – striedanie dňa a noci.
Mesiac – striedanie mesačných fáz na oblohe.
Rok – striedanie ročných období.
Vo všetkých prípadoch zodpovedá jednotka času nejakému periodicky sa opakujúce deji.
Postupom času sa objavila potreba deliť čas na kratšie úseky:
• hodina
• minúta
• sekunda.
Pr. 3: Dve z uvedených šiestich jednotiek nie sú považované za pravé fyzikálne jednotky. Ktoré to sú? Prečo? Mesiac a rok, pretože sa ich dĺžka mení.

Pr. 4: Zostav prevádzací schéma pre jednotky času (pravé fyzikálny).

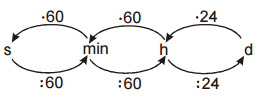
Dodatok: Delenie minút a hodín je pozostatkom dávneho používanie šesťdesiatkovej číselné sústavy v starovekom Sumeru pred 4000 rokmi. Je zaujímavé, že prežilo všetky revolúcia aj zavedenie metrickej sústavy jednotiek.
Pr. 5: Preveď na jednotku v zátvorke.

Pedagogická poznámka: Predchádzajúci príklad rieši žiaci samozrejme s kalkulačkou (buď normálnej alebo v mobile).
Pr. 6: prekreslí si do zošita obrázky nasledujúcich hodín. Nezabudni na nič podstatné pre ich funkciu. Pri každom type vysvetli, ako funguje.

Meranie času je založené na dejoch, ktoré sa pravidelne opakujú.
Pr. 7: Aké ďalšie druhy hodín poznáš?
Kyvadlové: kyvadlo sa kôň kýva zo strany na stranu (zakaždým za rovnako dlhú dobu) a tým ovláda otáčanie ručičiek.
Slnečné: tieň tyčky sa pohybuje podľa pohybu slnka po oblohe a ukazuje na číselníku čas.
Digitálne hodiny: obsahujú malý kryštál, ktorý po pripojení na elektrický prúd začne veľmi rýchlo a veľmi pravidelne kmitať. Jeho kmitanie riadi chod hodín (takto je dneska riešená veľká
väčšina hodina).
Atómové hodiny: využívajú pravidelné kmitanie atómov (veľmi malých čiastočiek hmoty).

Pr. 8: Pomocou obrázku sa pokus vysvetliť, akým spôsobom riadi kyvadlo chod kyvadlových hodín.

Pr. 9: Preveď na jednotku v zátvorke.

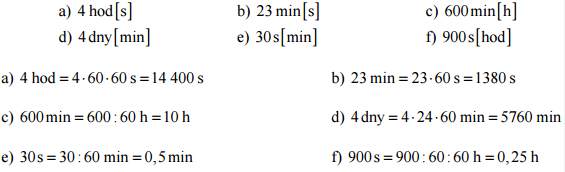
Domáce bádania: Chod kyvadlových hodín určuje kyvadlo. Zostroj kyvadlo z ťažkej matice (Alebo iného malého predmetu) zaveseného na tenkom povrázku. Od čoho závisí doba, po
ktorou sa kyvadlo pohybu tam a späť (čas kmitu)? Zostroj kyvadlo ktorého doba kmitu je presne 1 s.
Zhrnutie: Všetky typy hodín využívajú niektorý z pravidelne sa opakujúcich dejov.

Pr. 1: Nakresli z pamätí schéma pre prevádzanie jednotiek objemu.
Pr. 2: Preveď na jednotku v zátvorke.

Pr. 3: Preveď na jednotku v zátvorke.

Pr. 4: Preveď na jednotku v zátvorke.

Pr. 5: Navrhni, ako určiť objem kameňa, ktorý je príliš veľký, nezmestí sa do žiadneho odmerného valca, ale zmestí sa do vedra na vodu.
Pr. 6: Máme k dispozícii dve nádoby. Druhá nádoba má dvakrát menší priemer než prvá nádoba. Koľko vyššia bude vodný stĺpec v druhej nádobe? Over odhad pokusom a vysvetli výsledok.
Pr. 7: Jedna stopa má dĺžku 30,48 cm. Koľko má jedna kubická stopa (objem kocky o hrane 1 stopa) litrov?
Pr. 8: Koľko bude stáť nákup ôsmich hranolov s rozmermi 10 x 10 cm x 4,5 m na opravu stropu, ak je v cenníku píly uvedené
Smrekové hranoly: do 6m dĺžky 6.300 € / m3 cena bez DPH
Cenu s DPH, ktorú musíme platiť, získame z ceny bez DPH tak, že ju vynásobíme 1,2.
Pr. 9: Jedným z návrhov ako riešiť nedostatok vody v niektorých krajinách je využitie polárnych ľadovcov (je v nich ukrytá väčšina sladkej vody na Zemi). Ľadovec by sa zavaril do obale z umelej hmoty a vlečná loď by ho odtiahla po mori. U pevniny by ľadovec postupne tál a voda by sa odčerpávala z obalu do vodovodu. Na ako dlho by

Pomôcky: odmerné valce, 8 kociek
Pr. 1: Nakresli z pamätí schéma pre prevádzanie jednotiek objemu.
Schéma pre prevádzanie jednotiek objemu:
• dve riadky:
kubické jednotky (mm³, …), základný krok 1000,
objemovej jednotky odvodené z litra, základný krok 10,
• 1dm³ = 1 l.

Pedagogická poznámka: Bavíme sa o tom, ako málo si toho musíme pamätať, aby sme schéma nakreslili.
Pr. 2: Preveď na jednotku v zátvorke.

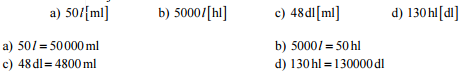
Pr. 3: Preveď na jednotku v zátvorke.

Pr. 4: Preveď na jednotku v zátvorke.

Pr. 5: Navrhni, ako určiť objem kameňa, ktorý je príliš veľký, nezmestí sa do žiadneho odmerného valca, ale zmestí sa do vedra na vodu. Naplníme kýbel úplne vodou. Teraz môžeme postupovať rôzne:
• Do vedra pomaly položíme kameň a necháme vytiecť vodu. Potom dolievame do vedra vodu o známych objemoch, kým nebude plný. Súčet objemov, ktoré sme do vedra dolial sa rovná objemu kameňa.
• Kýbeľ položíme do väčšej nádoby, tak aby táto nádoba zachytila vodu, ktorá z kýblu vytečie potom, čo do neho položíme kameň. Zmeriame objem vypustenej vody, ktorý je rovný objemu kameňa.
Pr. 6: Máme k dispozícii dve nádoby. Druhá nádoba má dvakrát menší priemer než prvá nádoba. Koľko vyššia bude vodný stĺpec v druhej nádobe? Over odhad pokusom a vysvetli výsledok.
V druhej nádobe vystúpi voda do dvojnásobnej výšky.
Výsledok pokusu: Voda v druhej nádobe vystúpi do výšky, ktorá je približne štvornásobná.
Vysvetlenie: Prvá nádoba má dvakrát väčší polomer, čo znamená, že sa do jednej vrstvy vojde štyrikrát viac vody ⇒ vodný stĺpec bude štyrikrát nižšia ako u druhej nádoby.
Situáciu si môžeme ukázať aj na kockách. Veža vľavo má dvakrát väčšiu stranu základne ako veža vpravo a preto musí byť štyrikrát nižšia, aby bola postavená z rovnakého počtu kociek.

Pedagogická poznámka: Ak niekto v predchádzajúcom príklade navrhne štyrikrát vyšší vodný stĺpec, je to naozajstná výnimka, väčšinou sa všetci zhodnú, že v druhej nádobe vystúpi voda dvakrát vyššie. Pokiaľ nikto nepríde na súvislosť so stavaním kocky s kociek, nechám príklad na rozmyslenie na budúci hodinu.
Pr. 7: Jedna stopa má dĺžku 30,48 cm. Koľko má jedna kubická stopa (objem kocky o hrane 1 stopa) litrov?
Vieme, že1 l =1 dm³ ⇒ prevedieme si dĺžku stopy na decimetre: 30, 48cm = 3,048dm.
Potrebujeme spočítať objem kocky s dĺžkou strany 3,048dm.
V = a * a * a = 3,048 * 3,048 * 3,048 dm³ = 28,3 dm³ = 28,3 l
Jedna kubická stopa má objem 28,3 l.
Pr. 8: Koľko bude stáť nákup ôsmich hranolov s rozmermi 10 x 10 cm x 4,5 m na opravu
stropu, ak je v cenníku píly uvedené

Smrekové hranoly: do 6 m dĺžky 6.300 € / m³ cena bez DPH
Cenu s DPH, ktorú musíme platiť, získame z ceny bez DPH tak, že ju vynásobíme 1,2.
Z cenníka je jasné, že drevené hranoly sa platí za objem ⇒ musíme vypočítať objem všetkých hranolov.
Všetky rozmery prevedieme na metre: 0,1 x 0,1 x 4,5 m
V = a * b * c = 0,1 * 0,1 * 4,5 dm = 0,045 m³ objem jedného hranola.
Osem hranolov: 8 * 0,045 = 0,36 m³.
Cena dreva bez DPH: 6300 * 0,36 = 2268 €.
Cena dreva s DPH: 2268 * 1,2 = 2722 €.
Za osem stropných hranolov zaplatíme 2722 Kč.
Pr. 9: Jedným z návrhov ako riešiť nedostatok vody v niektorých krajinách je využitie polárnych ľadovcov (je v nich ukrytá väčšina sladkej vody na Zemi). Ľadovec by sa zavaril do obale z umelej hmoty a vlečná loď by ho odtiahla po mori. U pevniny by ľadovec
postupne tál a voda by sa odčerpávala z obalu do vodovodu. Na ako dlho by vystačila pre mesto s miliónom obyvateľov voda z ľadovca s rozmermi 3 x 1 x 1 km?
Objem vody, ktorá vnikne topením, je o desatinu menej ako objem ľadu. obyvatelia bohatších krajín v súčasnosti spotrebujú okolo 100 litrov pitnej vody denne.
Objem ľadu: V = a * b * c = 3 * 1 * 1 km = 3 km.
Desatina objemu ľadu:
0,3km ⇒ objem vody 3 -0,3 km³ = 2,7 km³.
Množstvo vody spotrebovanej obyvateľmi mesta:
100000000 l = 100000000 dm³ = 100000 m³ = 0,0001km³
Počet dní: 2,7: 0,0001 = 27000dní = 74-ročná
Voda z ľadovca by mestu stačila na 74 rokov. Ľudia v bytových domoch majú určite jeden typ merača na meranie objemu: vodomer (prípadne plynomer).

Domáce bádania: Nájdi vodomer (ak ho máte) a zmeraj týždenné spotrebu vody v celej domácnosti

Domáce bádania: Zmeraj koľko vody spotrebuješ pri kúpaní (sprchovanie)?
Zhrnutie: Pri prevádzaní kubických jednotiek je základný krok 1000 (nie 10).

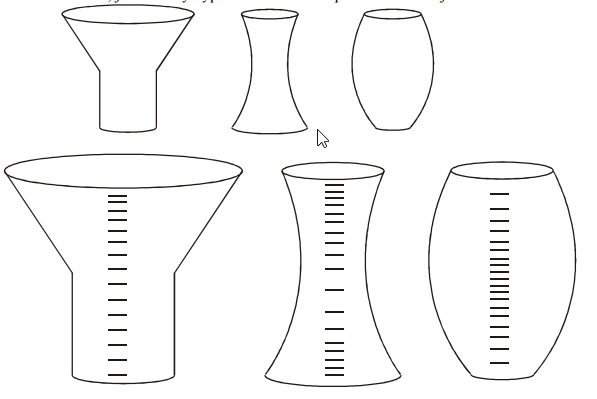
Pr. 1: Do rôznych nádob nalievame rovnaké množstvo vody. Od čoho závisí výška jej hladiny. Porovnaj výšku, do ktorej vystúpi voda vo vystavených nádobách.
Pr. 2: Porovnaj stupnica odmerných valcov, ktorých si doma vytvoril. Čím sa líšia? Prečo?
Pr. 3: Stupnica, ktorú si získal na svojich odmerných valcoch umožňuje merať iba s presnosťou, ktorá zodpovedá veľkosti nádobky, z ktorej si nalieval vodu. je možné stupnici ešte spresniť? Je to možné u oboch odmerných valcov? Prečo?
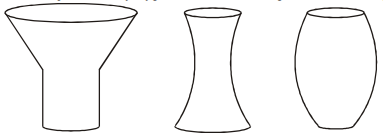
Pr. 4: načrtne, ako bude by vyzerala odmerná stupnica na nasledujúcich nádobách.

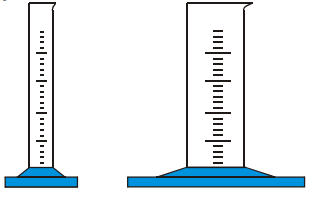
Pr. 5: Ktorý z odmerných valcov bude merať presnejšie? Prečo? Čím za väčšiu presnosť merania platíme?

Pr. 6: Zmeraj objem kúsku plastelíny.
Pr. 7: plastelínou vyber z odmerného valca, stlač ju. Zmení sa tým jej objem? svoj odhad potvrď pokusom.
Pr. 8: plastelínou vyber z odmerného valca a roztrhni ju na kusy. Zmení sa celkový objem
všetkých kúskov? Svoj odhad over pokusom.
Pr. 9: Typický automobil má pri jazde mimo mesta spotrebu 6 litrov benzínu na 100 km.
Odmeraj do svojho odmerného valca objem vody, ktorý je rovnaký ako objem benzínu, na ktorý auto prejde 1 km.

Pr. 10: Preveď na jednotku v zátvorke.

Pomôcky: odmerné valce z domova, hrnčeky, plastelína, odmerné valce
Pedagogická poznámka: Počas práce na nasledujúcich príkladoch posielam po triede dva
odmerné valce, z ktorých má každý odpočítať hodnotu objemu.
Pr. 1: Do rôznych nádob nalievame rovnaké množstvo vody. Od čoho závisí výška jej hladiny. Porovnaj výšku, do ktorej vystúpi voda vo vystavených nádobách.
Výška hladiny vody v nádobách závisí na tom, ako sú nádoby široké. Čím je nádoba širší, tým vyššie voda vystúpi ⇒ najviac voda vystúpi v najužšej nádobe, v najširšej nádobe bude
voda najnižšie.
Pr. 2: Porovnaj stupnica odmerných valcov, ktorých si doma vytvoril. Čím sa líšia? Prečo? Na odmernom valci s kolmými stenami sú všetky dieliky od seba rovnako ďaleko. na
odmernom valci z téglika (s rozširujúcimi sa stenami) sú vyššie dieliky bližšie pri sebe (tým sú dieliky vyššie, tým bližšie sú navzájom).
Ako sa téglik postupne rozširuj, každý ďalší kúsok vody tak nalievame do väčšej nádoby a on tak vytvára nižší stĺpec.
Pr. 3: Stupnica, ktorú si získal na svojich odmerných valcoch umožňuje merať iba s presnosťou, ktorá zodpovedá veľkosti nádobky, z ktorej si nalieval vodu. je možné stupnici ešte spresniť? Je to možné u oboch odmerných valcov? Prečo?
Odmerný valec s kolmými stenami: dieliky sú od seba rovnako ďaleko ⇒ vzdialenosti medzi nimi môžeme rozdeliť na polovicu (tretinu, štvrtinu, …) a získame tak presnejšie odmerný
valec. Odmerný valec s rozširujúcimi sa stenami: dieliky sú od seba rôzne ďaleko ⇒ vzdialenosti medzi nimi by sme museli deliť nejakým zložitejším spôsobom ⇒ nedokážeme tento odmerný valec spresniť.

Pr. 4: načrtne, ako bude by vyzerala odmerná stupnica na nasledujúcich nádobách.

Čím je nádoba v danom mieste širšie, tým hustejšie sú dieliky na stupnici.
Pr. 5: Ktorý z odmerných valcov bude merať presnejšie? Prečo? Čím za väčšiu presnosť merania platíme?

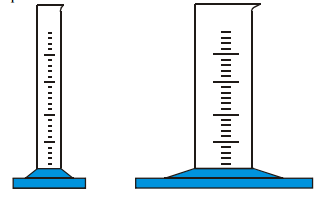
Presnejšie bude merať užšie valec (dieliky, ktoré predstavujú rovnako veľký objem, sú od seba viac vzdialené a môžeme ich ľahšie rozlíšiť).
Nevýhody úzkych odmerných valcov:
• okrem kvapalín môžeme merať len objemy malých pevných predmetov (väčšie sa do
odmerného doske nezmestí),
• môžeme merať len malé objemy (alebo musí byť valec veľmi vysoký).
Pekným prípadom meracieho valca s rozširujúcimi sa stenami je odmerka na moč.

Všetky dieliky na obrázku znamenajú 10 ml.
Pr. 6: Zmeraj objem kúsku plastelíny.
Zmeriame objem ľubovoľného množstva vody v odmernom valci. Potom do odmerného valca hodíme modelínu a znovu meriame objem. Objem modelíny vypočítame ako rozdiel nameraných hodnôt.
Pr. 7: plastelínou vyber z odmerného valca, stlač ju. Zmení sa tým jej objem? Svoj odhad potvrď pokusom.
Objem plastelíny sa nezmení. Pokus potvrdil náš odhad.
Pr. 8: plastelínou vyber z odmerného valca a roztrhni ju na kusy. Zmení sa celkový objem
všetkých kúskov? Svoj odhad over pokusom.
Celkový objem všetkých kúskov plastelíny je rovnaký ako pôvodný objem celej plastelíny.
Pr. 9: Typický automobil má pri jazde mimo mesta spotrebu 6 litrov benzínu na 100 km. Odmeraj do svojho odmerného valca objem vody, ktorý je rovnaký ako objem benzínu, na ktorý auto prejde 1 km.
Na prejdení 1 km potrebujeme stokrát menej benzínu ako na prejdenie 100 km ⇒ potrebujeme 0,06 6cl l = benzínu.
Ak jeden diele zodpovedá malému Štamprle (2 cl) ide o objem troch dielikov.
Pedagogická poznámka: Väčšina žiakov sa čudujú, že stačí tak málo.

Pedagogická poznámka: S prevodom v nasledujúcich príkladoch začíname na konci hodiny, takže sa dá očakávať, že väčšina triedy bude musieť príklady dorobiť doma.
Pr. 10: Preveď na jednotku v zátvorke.

Pr. 1: Odhadni (výpočty) objem triedy.
Pr. 2: Koľkokrát by sa objem triedy zväčšil, keby sa všetky jej rozmery zväčšili dvakrát (Trieda by sa zväčšila na dvojnásobok)? Koľkokrát by objem triedy zväčšil, keby sa všetky rozmery zväčšili desaťkrát?
Pr. 3: Koľko kociek potrebuješ, aby si zostavil kocku s strane, ktorá je dvakrát väčšia ako
hrana kocky.
Pr. 4: Nakresli obrázok kocky s dĺžkou hrany 1 dm. Koľko takých kocôčok potrebuješ, aby si zostavil kocku s hranou 1m (teda kocku s objemom 3
1m)?
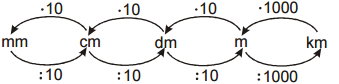
Pr. 5: Prevody medzi jednotkami dĺžky sme zapísali do prehľadného schémy.

Zostáv podobné schéma pre prevody jednotiek objemu.
Pr. 6: Poznáš jednotky objemu, ktoré v prehľade chýba?
Pr. 7: Zostav prevodné schéma po jednotky, ktoré v sebe nesú slovo liter. Prečo sa používajú tieto jednotky a nevystačíme s jednotkami odvodenými od dĺžky 1 meter.
Pr. 8: Môžeme vytvoriť medzi oboma skupinami ďalšie spojenie medzi jednotkami, ktoré udávajú rovnaký objem?

Pr. 9: Nájdi si v učebnici na strane 42 postup, akým meriame objem pomocou odmerného valce a zapíš ho do zošita (stručne).
Pr. 10: Preveď na litre.

Pr. 11: Preveď na jednotku v zátvorke.

Pr. 12: Preveď na jednotku v zátvorke.

Pr. 13: Preveď na jednotku v zátvorke.

Domáce bádania: Nalej z jedného pohára rovnaký objem do rôzne veľkých nádob. Prečo voda nevystúpi vždy do rovnakej výšky? Dokážeš dopredu odhadnú, v ktorej nádobe vystúpi voda vyššie ako v inej? V akých nádobách vystúpi voda vyššie než v pôvodnej poháriku?
Domáce bádania: Výroba vlastného meracieho valca nie je zložitá. Vezmeš si malú nádobu (Napríklad štamprle), naplníš ho vodou po značku a potom vodu přeliješ do nádoby, z ktorej chceš vyrobiť odmerný valec. Hladinu vody vyznačíš fixkou. Rovnako pokračuješ aj ďalej. po každom doliatie vody zakreslíš aktuálnu výšku hladiny.Vyrob týmto spôsobom dva odmerné valce – jeden z nádoby s kolmými stenami (malá zaváranie, pohár od jogurtu, malá PET fľaša) a druhý z nádoby, ktorá sa rozširuje (väčšina téglikov od mliečnych výrobkov, najvhodnejšie sú tégliky od Bobíka Max alebo od Ehrmann Bobiččin jogurt – ide o to, aby sa téglik čo najviac rozširoval a bol aspoň proti svetlu čiastočne priehľadný).

Pomôcky: odmerné valce, 8 kociek
Objem – veľkosť časti priestoru, ktorý predmet zaberá.
Pedagogická poznámka: Pojem objemu žiaci formulujú spoločne. Snažím sa, aby používali príklady (predmet s malým a veľkým objemom, nafukovaním sa objem balónika zväčšuje) skôr než vety, ktoré sa tvária ako vedecké definície.
Pedagogická poznámka: Žiaci nejaké povedomie o výpočte objemu majú. Rozmery triedy najskôr spoločne odhadneme a až potom ich nechám počítať nasledujúce tri príklady. Jednotku riešime až potom.
Pr. 1: Odhadni (výpočty) objem triedy.
V = abc = 6 *10 * 4 = 240
Pr. 2: Koľkokrát by sa objem triedy zväčšil, keby sa všetky jej rozmery zväčšili dvakrát (Trieda by sa zväčšila na dvojnásobok)? Koľkokrát by objem triedy zväčšil, keby sa všetky rozmery zväčšili desaťkrát?
V = abc =  2 * 6 * 2 * 10 * 2 * 4 = 2 * 2 * 2 * 6 * 10 * 4 = 8 240 = 1920
Hoci sa každý z rozmerov triedy zväčšil iba dvakrát, celý objem triedy sa zväčšil osemkrát.
Zrejme preto že dvojnásobné zväčšenie rozmerov prehovorilo do vzorca celkom trikrát.
Keby sme zväčšili veľkosti strán desaťkrát, objem triedy by sa zväčšil 10 * 10 * 10 = 1000 tisíckrát.

Pedagogická poznámka: Skutočnosť, že sa objem triedy zväčší osemkrát väčšinu žiakov prekvapí, preto nasleduje ďalší príklad s kockami.
Pedagogická poznámka: Využitie komutativnosti násobenie žiakov samozrejme nenapadne, ukazujem ho na tabuľu a pripomínam, že ide o využitie vlastnosti, o ktoré sa (s veľkou
pravdepodobnosťou) bavili pred nedávnom v matematike.
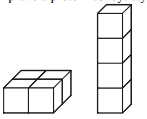
Pr. 3: Koľko kociek potrebuješ, aby si zostavil kocku s strane, ktorá je dvakrát väčšia ako hrana kocky.
Staviame väčšie kocku:
Potrebujeme 8 kociek.

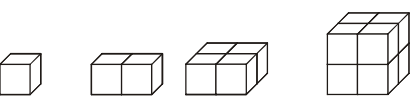
Zatiaľ sme spočítali dva objemy:

• trieda: 240
• dvojnásobná trieda (trieda – hangár): 1920
V našich výsledkoch niečo chýba – jednotka.
Pedagogická poznámka: Pokiaľ si nikto v triede nevšimne, že u našich výsledkov niečo chýba, spýtam sa sám.
Jednotkou objeme nemôže byť 1 m – jeden meter je vzdialenosť nie objem. Napriek tomu by bolo šikovné vystavať jednotku objemu na dĺžke 1 m. Aký najjednoduchšie objem môžeme vytvoriť
pomocou vzdialenosti 1 m?
Môžeme postaviť kocku s hranou 1 m, jej objem potom bude

V = 1* 1 *1 = 1.
Základnou jednotkou objemu je 3
1 m * 1 m * 1 m = 1 meter kubický.
Trojka v hornom indexe zachytáva:
• skutočnosť, že sme pri jej vytváraní trikrát násobilo meter,
• fakt, že priestor, ktorého časť kocky zaberá má tri rozmery (šírku, dĺžku výšku).
Pedagogická poznámka: V tomto okamihu nemá rozhodne cenu začať hovoriť o mocninách (Z matematiky o nich žiaci nič nevie).
Ako budeme prevádzať jednotky objemu? Príklad zo triedou napovedá, že to nebude tak jednoduché.
Pr. 4: Nakresli obrázok kocky s dĺžkou hrany 1 dm. Koľko takých kocôčok potrebuješ, aby si zostavil kocku s hranou 1m (teda kocku s objemom 1 meter kubický)?

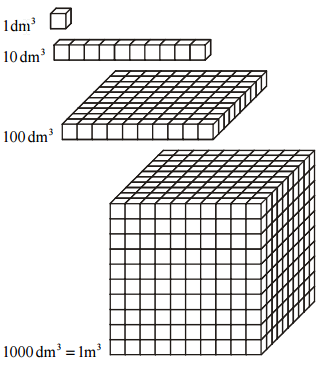
Platí teda 1 meter kubický = 1000 decimetrov kubických

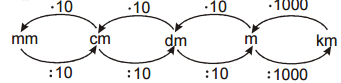
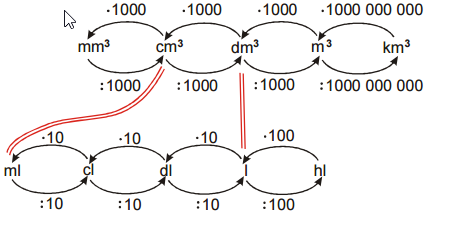
Pr. 5: Prevody medzi jednotkami dĺžky sme zapísali do prehľadného schémy.

Zostáv podobné schéma pre prevody jednotiek objemu.
Pri prevádzaní medzi susednými jednotkami teraz násobíme (delíme) tisíckou. pri prevádzaní medzi metery kubickými a
kilometery kubickými násobíme (delíme) miliardou.

Pedagogická poznámka: Väčšinu schémy žiaci vyplní správne, ale v prevádzaní medzi meterem kubickým kilometerem kubickým je správnych riešení len veľmi málo. Väčšinou píšu miesto miliardy 100 000, aby bol výmenný kurz sa opäť stokrát väčšia ako u ostatných jednotiek. Je dobré o tom stratiť slovo (Dôležité sú podobnosti, ktoré majú logický základ – napríklad zostavovanie kocky z menších kociek) a potom ich nechať predstaviť si, ako zostavujú kocku s hranou kilometera kubického o hrane
metera kubickýho. Veľmi rýchlo tak uvidia, že kockou budú potrebovať podstatne viac než len 100 000.
Pr. 6: Poznáš jednotky objemu, ktoré v prehľade chýba?
Objem sa tiež meria v litroch, hektolitroch alebo decilitroch.
Pr. 7: Zostav prevodné schéma po jednotky, ktoré v sebe nesú slovo liter. Prečo sa používajú tieto jednotky a nevystačíme s jednotkami odvodenými od dĺžky 1 meter.

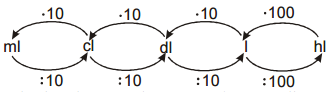
Jednotky odvodené od 1 metra majú „moc veľké medzery“ (každá jednotka je minimálne tisíckrát väčšie ako jej menší sused).
Používať dve sady jednotiek, ktoré nie sú nijako zviazané by bolo dosť nepohodlné (išlo by o návrat do stredoveku, kedy mal každý svoje jednotky) ⇒ musí existovať jednoduchý spôsob, ako
prevádzať litre na niektorú z jednotiek odvodených z metra ⇒ platí:

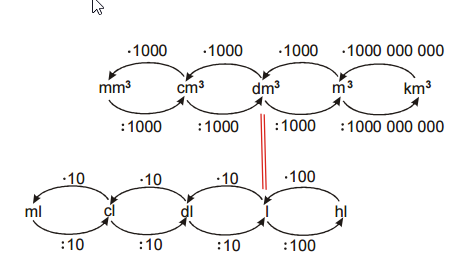
Pr. 8: Môžeme vytvoriť medzi oboma skupinami ďalšie spojenie medzi jednotkami, ktoré udávajú rovnaký objem?
• 1 centimeter kubický je tisíckrát menšia ako decimeter kubický
• 1ml je tisíckrát menšia ako 1l,
platí:  1 centumeter kubický = 1 ml

Objem nemusíme vždy len počítať, u kvapalín, plynov alebo sypkých ho môžeme aj priamo merať pomocou nádob s vyznačeným objemom – napríklad pivo i limonády sa v
reštauráciách nalievajú do nádob s ryskou, ktorá umožňuje kontrolovať, či nás nesklamú.
Vo fyzike a chémii potom používame špeciálne nádoby, na ktorých je rysiek kopa – odmerné vojne.
Pr. 9: Nájdi si v učebnici na strane 42 postup, akým meriame objem pomocou odmerného valce a zapíš ho do zošita (stručne).
1. Valec stojí vodorovne.
2. Pozeráme sa v rovine hladiny.
3. odčítajú podľa rovné (spodnej) časti hladiny.
Poznámka: Písmenko l, ktoré sa používa na označenie 1 litra. bohužiaľ veľmi pripomína číslo 1, preto v miestach, kde by mohlo dôjsť k nejasnostiam, či ide o písmeno l alebo číslo 1, píšem l
kurzívou l.

Pedagogická poznámka: Času na prevádzanie veľa nebude, treba prevádzanie ukončiť tak, aby ešte zostal čas prejsť a prípadne dovysvětlit domáce bádania. Tentoraz je povinné a bude sa naň nadväzovať ďalšiu hodinu.
Pr. 10: Preveď na litre.

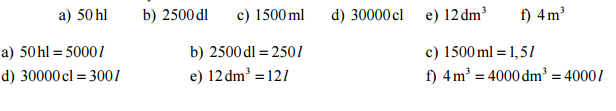
Pr. 11: Preveď na jednotku v zátvorke.

Pr. 12: Preveď na jednotku v zátvorke.

Pr. 13: Preveď na jednotku v zátvorke.

Domáce bádania: Nalej z jedného pohára rovnaký objem do rôzne veľkých nádob. Prečo voda nevystúpi vždy do rovnakej výšky? Dokážeš dopredu odhadnú, v ktorej nádobe vystúpi
voda vyššie ako v inej? V akých nádobách vystúpi voda vyššie než v pôvodnej poháriku?

Domáce bádania: Výroba vlastného meracieho valca nie je zložitá. Vezmeš si malú nádobu (Napríklad štamprle), naplníš ho vodou po značku a potom vodu přeliješ do nádoby, z ktorej
chceš vyrobiť odmerný valec. Hladinu vody vyznačíš fixkou. Rovnako pokračuješ aj ďalej. po každom doliatie vody zakreslíš aktuálnu výšku hladiny.Vyrob týmto spôsobom dva odmerné
valce – jeden z nádoby s kolmými stenami (malá zaváranie, pohár od jogurtu, malá PET fľaša) a druhý z nádoby, ktorá sa rozširuje (väčšina téglikov od mliečnych výrobkov, najvhodnejšie sú tégliky od Bobíka Max alebo od Ehrmann Babičkin jogurt – ide o to,
aby sa téglik čo najviac rozširoval a bol aspoň proti svetlu čiastočne priehľadný).
Žiaci prinesú nabudúce: vyrobené odmerné valce, téglik.