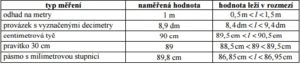
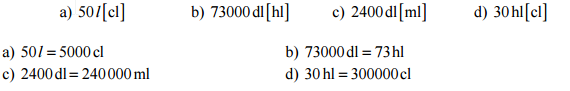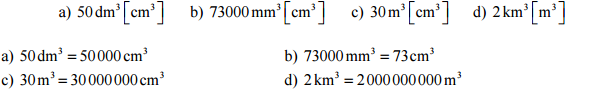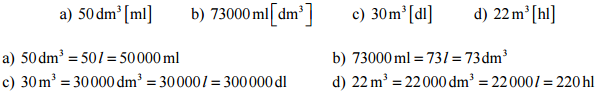Pomôcky: odmerné valce, 8 kociek
Objem – veľkosť časti priestoru, ktorý predmet zaberá.
Pedagogická poznámka: Pojem objemu žiaci formulujú spoločne. Snažím sa, aby používali príklady (predmet s malým a veľkým objemom, nafukovaním sa objem balónika zväčšuje) skôr než vety, ktoré sa tvária ako vedecké definície.
Pedagogická poznámka: Žiaci nejaké povedomie o výpočte objemu majú. Rozmery triedy najskôr spoločne odhadneme a až potom ich nechám počítať nasledujúce tri príklady. Jednotku riešime až potom.
Pr. 1: Odhadni (výpočty) objem triedy.
V = abc = 6 *10 * 4 = 240
Pr. 2: Koľkokrát by sa objem triedy zväčšil, keby sa všetky jej rozmery zväčšili dvakrát (Trieda by sa zväčšila na dvojnásobok)? Koľkokrát by objem triedy zväčšil, keby sa všetky rozmery zväčšili desaťkrát?
V = abc = 2 * 6 * 2 * 10 * 2 * 4 = 2 * 2 * 2 * 6 * 10 * 4 = 8 240 = 1920
Hoci sa každý z rozmerov triedy zväčšil iba dvakrát, celý objem triedy sa zväčšil osemkrát.
Zrejme preto že dvojnásobné zväčšenie rozmerov prehovorilo do vzorca celkom trikrát.
Keby sme zväčšili veľkosti strán desaťkrát, objem triedy by sa zväčšil 10 * 10 * 10 = 1000 tisíckrát.
Pedagogická poznámka: Skutočnosť, že sa objem triedy zväčší osemkrát väčšinu žiakov prekvapí, preto nasleduje ďalší príklad s kockami.
Pedagogická poznámka: Využitie komutativnosti násobenie žiakov samozrejme nenapadne, ukazujem ho na tabuľu a pripomínam, že ide o využitie vlastnosti, o ktoré sa (s veľkou
pravdepodobnosťou) bavili pred nedávnom v matematike.
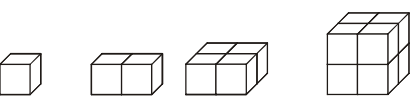
Pr. 3: Koľko kociek potrebuješ, aby si zostavil kocku s strane, ktorá je dvakrát väčšia ako hrana kocky.
Staviame väčšie kocku:
Potrebujeme 8 kociek.
Zatiaľ sme spočítali dva objemy:
• trieda: 240
• dvojnásobná trieda (trieda – hangár): 1920
V našich výsledkoch niečo chýba – jednotka.
Pedagogická poznámka: Pokiaľ si nikto v triede nevšimne, že u našich výsledkov niečo chýba, spýtam sa sám.
Jednotkou objeme nemôže byť 1 m – jeden meter je vzdialenosť nie objem. Napriek tomu by bolo šikovné vystavať jednotku objemu na dĺžke 1 m. Aký najjednoduchšie objem môžeme vytvoriť
pomocou vzdialenosti 1 m?
Môžeme postaviť kocku s hranou 1 m, jej objem potom bude
V = 1* 1 *1 = 1.
Základnou jednotkou objemu je 3
1 m * 1 m * 1 m = 1 meter kubický.
Trojka v hornom indexe zachytáva:
• skutočnosť, že sme pri jej vytváraní trikrát násobilo meter,
• fakt, že priestor, ktorého časť kocky zaberá má tri rozmery (šírku, dĺžku výšku).
Pedagogická poznámka: V tomto okamihu nemá rozhodne cenu začať hovoriť o mocninách (Z matematiky o nich žiaci nič nevie).
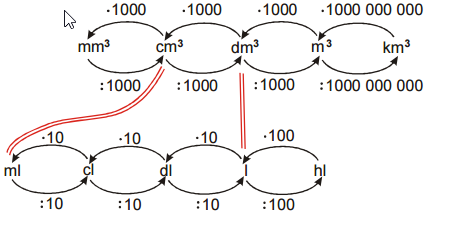
Ako budeme prevádzať jednotky objemu? Príklad zo triedou napovedá, že to nebude tak jednoduché.
Pr. 4: Nakresli obrázok kocky s dĺžkou hrany 1 dm. Koľko takých kocôčok potrebuješ, aby si zostavil kocku s hranou 1m (teda kocku s objemom 1 meter kubický)?
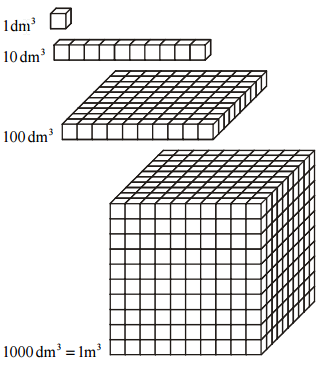
Platí teda 1 meter kubický = 1000 decimetrov kubických
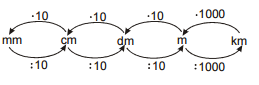
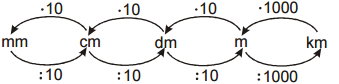
Pr. 5: Prevody medzi jednotkami dĺžky sme zapísali do prehľadného schémy.
Zostáv podobné schéma pre prevody jednotiek objemu.
Pri prevádzaní medzi susednými jednotkami teraz násobíme (delíme) tisíckou. pri prevádzaní medzi metery kubickými a
kilometery kubickými násobíme (delíme) miliardou.

Pedagogická poznámka: Väčšinu schémy žiaci vyplní správne, ale v prevádzaní medzi meterem kubickým kilometerem kubickým je správnych riešení len veľmi málo. Väčšinou píšu miesto miliardy 100 000, aby bol výmenný kurz sa opäť stokrát väčšia ako u ostatných jednotiek. Je dobré o tom stratiť slovo (Dôležité sú podobnosti, ktoré majú logický základ – napríklad zostavovanie kocky z menších kociek) a potom ich nechať predstaviť si, ako zostavujú kocku s hranou kilometera kubického o hrane
metera kubickýho. Veľmi rýchlo tak uvidia, že kockou budú potrebovať podstatne viac než len 100 000.
Pr. 6: Poznáš jednotky objemu, ktoré v prehľade chýba?
Objem sa tiež meria v litroch, hektolitroch alebo decilitroch.
Pr. 7: Zostav prevodné schéma po jednotky, ktoré v sebe nesú slovo liter. Prečo sa používajú tieto jednotky a nevystačíme s jednotkami odvodenými od dĺžky 1 meter.
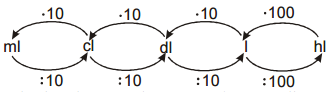
Jednotky odvodené od 1 metra majú „moc veľké medzery“ (každá jednotka je minimálne tisíckrát väčšie ako jej menší sused).
Používať dve sady jednotiek, ktoré nie sú nijako zviazané by bolo dosť nepohodlné (išlo by o návrat do stredoveku, kedy mal každý svoje jednotky) ⇒ musí existovať jednoduchý spôsob, ako
prevádzať litre na niektorú z jednotiek odvodených z metra ⇒ platí:
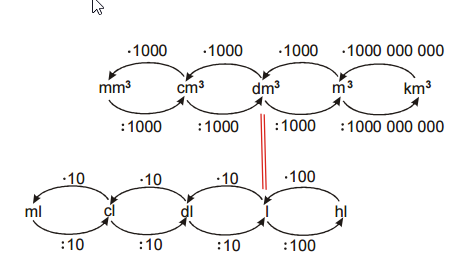
Pr. 8: Môžeme vytvoriť medzi oboma skupinami ďalšie spojenie medzi jednotkami, ktoré udávajú rovnaký objem?
• 1 centimeter kubický je tisíckrát menšia ako decimeter kubický
• 1ml je tisíckrát menšia ako 1l,
platí: 1 centumeter kubický = 1 ml
Objem nemusíme vždy len počítať, u kvapalín, plynov alebo sypkých ho môžeme aj priamo merať pomocou nádob s vyznačeným objemom – napríklad pivo i limonády sa v
reštauráciách nalievajú do nádob s ryskou, ktorá umožňuje kontrolovať, či nás nesklamú.
Vo fyzike a chémii potom používame špeciálne nádoby, na ktorých je rysiek kopa – odmerné vojne.
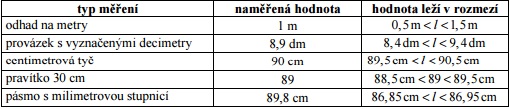
Pr. 9: Nájdi si v učebnici na strane 42 postup, akým meriame objem pomocou odmerného valce a zapíš ho do zošita (stručne).
1. Valec stojí vodorovne.
2. Pozeráme sa v rovine hladiny.
3. odčítajú podľa rovné (spodnej) časti hladiny.
Poznámka: Písmenko l, ktoré sa používa na označenie 1 litra. bohužiaľ veľmi pripomína číslo 1, preto v miestach, kde by mohlo dôjsť k nejasnostiam, či ide o písmeno l alebo číslo 1, píšem l
kurzívou l.
Pedagogická poznámka: Času na prevádzanie veľa nebude, treba prevádzanie ukončiť tak, aby ešte zostal čas prejsť a prípadne dovysvětlit domáce bádania. Tentoraz je povinné a bude sa naň nadväzovať ďalšiu hodinu.
Pr. 10: Preveď na litre.
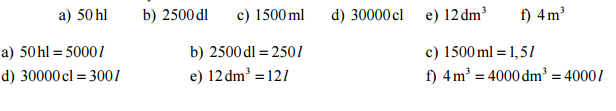
Pr. 11: Preveď na jednotku v zátvorke.
Pr. 12: Preveď na jednotku v zátvorke.
Pr. 13: Preveď na jednotku v zátvorke.
Domáce bádania: Nalej z jedného pohára rovnaký objem do rôzne veľkých nádob. Prečo voda nevystúpi vždy do rovnakej výšky? Dokážeš dopredu odhadnú, v ktorej nádobe vystúpi
voda vyššie ako v inej? V akých nádobách vystúpi voda vyššie než v pôvodnej poháriku?
Domáce bádania: Výroba vlastného meracieho valca nie je zložitá. Vezmeš si malú nádobu (Napríklad štamprle), naplníš ho vodou po značku a potom vodu přeliješ do nádoby, z ktorej
chceš vyrobiť odmerný valec. Hladinu vody vyznačíš fixkou. Rovnako pokračuješ aj ďalej. po každom doliatie vody zakreslíš aktuálnu výšku hladiny.Vyrob týmto spôsobom dva odmerné
valce – jeden z nádoby s kolmými stenami (malá zaváranie, pohár od jogurtu, malá PET fľaša) a druhý z nádoby, ktorá sa rozširuje (väčšina téglikov od mliečnych výrobkov, najvhodnejšie sú tégliky od Bobíka Max alebo od Ehrmann Babičkin jogurt – ide o to,
aby sa téglik čo najviac rozširoval a bol aspoň proti svetlu čiastočne priehľadný).
Žiaci prinesú nabudúce: vyrobené odmerné valce, téglik.