Pr. 1: Navrhni fyzikálny jav, ktorý by sme mohli využiť na objektívnemu meranie teploty.
Pr. 2: Ako sa mení vzduch vo fľaši počas pokusu? Ako by sme mohli túto vlastnosť využiť pre meranie teploty?
Pr. 3: Ako reaguje voda na zmenu teploty? Je možné tento pokus využiť ku konštrukcii v praxi používaného teplomeru?
Pr. 4: Môže byť látkou, ktorá sa používa vo vonkajších teplomeroch voda? Prečo?
Pr. 5: Akú najvyššiu teplotu by sme mohli merať v kvapalinovom teplomere s vodou?
Pr. 6: Teplotu meriame v stupňoch Celzia. Skús si spomenúť na zaujímavú zhodu teploty v stupňoch Celzia niektorých zaujímavých dejov. Akú má táto zhoda príčinu?
Pr. 7: Navrhni spôsob, ako na slepý teplomer nakresliť stupnicu pre meranie teploty vo stupňoch Celzia.
Pr. 8: Navrhni spôsob, ako merať pomocou dilatačné škáry mosta merať teplotu).
Pr. 9: Na fotografii je model bimetalového (dvojkovového) teplomera. ide zakrútený opasok, zlepený z alobalu a papiera – tieto látky sa pri zvýšení teploty rozťahujú rôzne.
Ktorá z nich sa rozťahuje pri zvýšení teploty viac? (Alobal je na vonkajšej strane pásku, opasok sa pri zahriatí viac zakrúti).
Pr. 10: narysujte na celú výšku stránky teplotnú stupnicu a do nej vyznač nasledujúce teploty:
a) najnižšia teplota nameraná na Zemi: – ° 89, 2 C, Vostok, Antarktída, 1983,
b) najnižšia teplota nameraná v SR: – ° 42, 2 C, Litvínovice 1929,
c) najvyššia teplota nameraná na Zemi: 56,7 C °, Death Valey, USA, 1913,
d) najvyššia teplota nameraná v SR: 40,4 C °, Dobřichovice 2012,
e) teplota varu vody 100 C °, f) teplota topenia ľadu 0 C °,
g) teplota topenia liehu h) teplota varu liehu
Všetky príspevky Patrik
Meriame teplotu
Pomôcky: kahan, stojan, voda, bimetal z alobalu a papiera, sklenená fľaša, slamku, plastelína, PET mäkká, teplomer, ľad, vŕtačka, doštička, drevený kolík do nábytku
Domáce pokus:
Priprav si tri hrnca. Do jedného nalej studenú vodu (môžeš aj přihladit ľadom z chladničky), do druhého vlažnú vodu a do tretieho horúcu vodu (takú, aby si v nej mohol držať ruku). Jednu ruku ponor do nádoby so studenou vodou, druhú do nádoby s horúcou vodou. Asi po minúte prelož obe ruky do prostrednej nádoby. Čo cítiš?
Ruky vo vlažnej vode sa hádali.
• ruka, ktorá bola predtým v studenej vode, cíti, že vlažná voda je teplá,
• ruka, ktorá bola predtým vo horúcej vode, cíti, že vlažná voda je studená, ⇒ obe ruky klamú, pretože voda v prostrednom hrnci má jednu teplotu. Záver: Človek vníma teplotu, ale nie je dobrý teplomer. Naše vnímanie je nastavené tak, že dobre vnímame zmeny teploty (rovnako to platí aj u iných veličín napríklad hluku), ale zle
jej aktuálnu hodnotu:
• ruka, ktorá bola predtým v studenej vode, cíti, že sa dostala do teplejšej vody a preto ju cíti, ako teplú,
• ruka, ktorá bola predtým vo horúcej vode, cíti, že sa dostala do studenšie vody a preto ju cíti ako studenú.
Vo fyzike sa nemôžeme spoľahnúť na meranie teploty ľudským odhadom ⇒ musíme nájsť iné spôsoby merania teploty, ktoré nezávisia na našich pocitoch.
Pedagogická poznámka: Pokus v škole nevykonávame, pri diskusii na stole samozrejme demonštrujem rukami.
Aké výhody má uvedený spôsob vnímania teploty pre náš život?
Uvedené vnímanie teploty nám umožňuje si zvyknúť na okolité prostredie a teplotu nevnímať.
Pr. 1: Navrhni fyzikálny jav, ktorý by sme mohli využiť na objektívnemu meranie teploty. Mohli by sme využiť druhý domáci pokus, s uzavretou fľašou plnou vzduchu.
Prázdna (teda plná vzduchu) uzavretá fľaša:
• fľašu ochladíme studenou vodu: fľaša sa zmrští, po otvorení nasaje vzduch,
• fľašu ohrejeme horúcou vodou: fľaša sa nafúkne, po otvorení z nej uniká vzduch.
Pedagogická poznámka: Pokus si ukazujeme, výsledok nie je tak dobre vidieť, ako keď si žiaci vykonajú doma.
Pr. 2: Ako sa mení vzduch vo fľaši počas pokusu? Ako by sme mohli túto vlastnosť využiť pre meranie teploty?
• Pri zahrievaní sa zväčšuje objem vzduchu (vzduch sa rozťahuje).
• Pri ochladzovaní sa zmenšuje objem vzduchu (vzduch sa zmršťuje).
Môžeme merať objem vzduchu v uzavretej nádobe, čím väčší objem vzduchu tým väčšia je teplota.
Je zväčšovanie objem s rastom teploty špeciálnou vlastnosťou vzduchu, alebo sa podobne správajú aj iné látky?
Pokus:
Sklenenú fľašu od sirupu úplne naplníme zafarbenou studenú vodu, hrdlo upcháme kusom modelíny, do ktorej strčíme slamku. Fľaša dáme do hrnca s horúcou a vodou necháme ju zahrievať. Voda postupne stúpa Brcko a potom začne odkvapkávať.
Pr. 3: Ako reaguje voda na zmenu teploty? Je možné tento pokus využiť ku konštrukcii v praxi používaného teplomeru?
Pri zahrievaní sa objem vody zväčšuje ⇒ môžeme merať zmeny objemu a spoznať z nich teplotu.
Princíp sa využíva u vonkajších teplomerov, v trubičke je tekutina. Čím väčšia je jej teplota, tým väčšiu má objem, tým vyššie v trubičke dosahuje a tým väčšiu hodnotu odčítame na stupnici.
Pr. 4: Môže byť látkou, ktorá sa používa vo vonkajších teplomeroch voda? Prečo? Nemôže, voda sa pri 0 C ° mení na ľad (zmena na ľad znamená aj veľkú zmenu objemu).
Pr. 5: Akú najvyššiu teplotu by sme mohli merať v kvapalinovom teplomere s vodou? Najvyššia teplotou je 100 C °. Pri 100 C ° začne voda variť a prestane zväčšovať svoj objem. Vonkajší teplomer je príkladom kvapalinového teplomera: teplomer obsahuje kvapalinu, zmena jej objemu znamená zmenu výšky hladiny, výška hladiny ukazuje na stupnici teplotu vody.
Dve najčastejšie používané kvapaliny:
• lieh (vonkajšie teplomery),
• ortuť (lekársky teplomer).
Pr. 6: Teplotu meriame v stupňoch Celzia. Skús si spomenúť na zaujímavú zhodu teploty v stupňoch Celzia niektorých zaujímavých dejov. Akú má táto zhoda príčinu?
Dva fyzikálne deje majú „okrúhle“ hodnoty teploty v stupňoch Celzia:
• 0 C °: voda sa mení v ľad, ľad sa mení na vodu,
• 100 C °: voda varí.
Celziova stupnica je zrejme vymyslená tak, aby teplota 0 C ° zodpovedala topenia ľadu a teplota 100 C ° varu vody.
Mohli by sme na našom sklenenom teplomere merať teplotu?
Nemohli, pretože na ňom nemáme nakreslenú stupnici.
Pr. 7: Navrhni spôsob, ako na slepý teplomer nakresliť stupnicu pre meranie teploty vo stupňoch Celzia.
• Pomorie teplomer do vody s ľadom ⇒ označíme 0 C °,
3
• Pomorie teplomer do vriacej vody ⇒ označíme 100 C °, vzdialenosť medzi značkami rozdelíme na sto dielikov. Zväčšovanie objemu s teplotou nie je iba záležitosťou plynov a kvapalín. Objem a rozmery
zväčšujú aj pevné látky.
Divná komplikácie pri stavbách mostov:
• na začiatku a konci mosta býva škára (dilatačná špára – tu a tu),
• mosty bývajú postavené na valcoch.
Dôvod: Most sa pri zvýšení teploty zväčší ⇒
• potrebuje miesto, kam sa vojde (zaplní miesto dilatačné škáry),
• potrebuje možnosť sa pohnúť (mostovka sa môže pohybovať po valcoch).
Pr. 8: Navrhni spôsob, ako merať pomocou dilatačné škáry mosta merať teplotu). Vyššia teplota ⇒ dlhší most ⇒ viac zaplnená dilatačná špára ⇒ môžeme merať šírku škáry, čím bude škára dlhšia, tým je teplota nižšia.
Pr. 9: Na fotografii je model bimetalového (dvojkovového) teplomera. ide zakrútený opasok, zlepený z alobalu a papiera – tieto látky sa pri zvýšení teploty rozťahujú rôzne. Ktorá z nich sa rozťahuje pri zvýšení teploty viac? (Alobal je na vonkajšej strane pásku, opasok sa pri zahriatí viac zakrúti).
Materiál na vonkajšej strane je dlhšia ako na strane vnútornej ⇒ keď sa pásik snažia viac zakrútiť, materiál na vonkajšej strane sa viac predlžuje ⇒ alobal sa viac predlžuje ako papier.
Bimetal (z ozajstného bimetalu) sa často používajú: vypínajú ističe, varné kanvice, žehličky, …
Pr. 10: narysujte na celú výšku stránky teplotnú stupnicu a do nej vyznač nasledujúce teploty:
a) najnižšia teplota nameraná na Zemi: – 89, 2 °C, Vostok, Antarktída, 1983,
b) najnižšia teplota nameraná v SR: – 42, 2 °C, Litvínovice 1929,
c) najvyššia teplota nameraná na Zemi: 56,7 °C , Death Valey, USA, 1913,
d) najvyššia teplota nameraná v SR: 40,4 °C, Dobřichovice 2012,
e) teplota varu vody 100 °C , f) teplota topenia ľadu 0 °C ,
g) teplota topenia liehu h) teplota varu liehu
Žiaci prinesú nabudúce: zápalky
Archimedov zákon I – príklady
Pr. 1: Napíš výsledky domáceho bádania (ponáranie lopty do vody).
Pr. 2: Nakresli obrázok čiastočne ponoreného lopty, ktorý tlačí ruka pod vodu. Aké sily na lopta pôsobí?
Pr. 3: Lopta na vode pláva, pretože na neho voda pôsobí vztlakovou silou. Pôsobí voda aj na predmety, ktoré neplávajú?
Pr. 4: Chová sa voda pri nadľahčovanie neplavoucích predmetov podobne ako u lopty (jej vztlaková sila sa zväčšuje s ponorením predmetu)? Uveď príklad z vlastnej skúsenosti.
Pr. 5: Na obrázku je nakreslená sivá gulička. Je úplne ponorená do vody a je vyrobená tak, že sa vo vode vznáša (ani nestúpa k hladine, ani neklesá ku dnu). Aké sily na ňu pôsobí? Zakreslite ich do obrázka. Napravo od šedej guličky je naznačená vo vode vo rovnakej hĺbke rovnako veľká myslená guľa z vody (môžeš si predstaviť, že je od
ostatné vody oddelená tenkou blankou, ktorá prakticky nič neváži). Ako sa „vodná“ gulička pohybuje? Aké sily pôsobia na nej pôsobí?
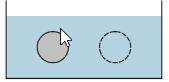
Pr. 6: Porovnaj veľkosti vztlakových síl v predchádzajúcom príklade. Ktoré sily a prečo majú rovnakú veľkosť ako vztlaková sila na šedú guličku?
Pr. 7: Na obrázkoch je nakreslené postupné ponáranie lopty do vody. Vyfarbi u každého okamihu Archimedovom teleso a vysvetli, prečo je vztlaková sila, ktorú voda vytláča loptu, pri väčšom ponorení väčší.
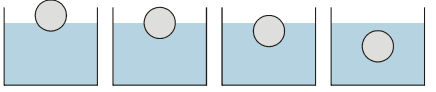
Pr. 8: On obrázkoch sú nakreslené rôzne predmety. Číslo u každého z nich udáva jeho objem. Akú vztlakovou silou bude každý z nich nadľahčovať voda, keď je úplne ponoríme? Akou silou ich budeme musieť do zatlačovať, aby zostali úplne ponorené?

Pr. 9: Máme k dispozícii k dispozícii predmet, ktorý vo vode klesá ku dnu, silomer, nádobu, dostatok vody a merací valec. Navrhni pokus, ktorým overíme platnosť Archimedovho zákona.
Pr. 10: Vo vode sú úplne ponorené dve rovnako veľké guľôčky. Jedna železná, druhá drevená. Pôsobí na obe rovnako veľká vztlaková sila vody? Čo sa stane, keď je pustíme? Prečo?
Pr. 11: Na hladine plávajú dve rovnako veľké guľôčky. Druhá je ponorená menej ako prvý. Ktorá z nich má menšiu hmotnosť?
Pr. 12: Čo je potrebné začať robiť, keď sa človek začne kúriť?
Archimedov zákon I
Pomôcky: voda, akvárium, loptička (alebo kus polystyrénu), súprava na demonštráciu Archimedovho zákona, Vernier silomer, čerstvé vajcia, pohár, soľ
Pr. 1: Napíš výsledky domáceho bádania (ponáranie lopty do vody).
Ponáranie lopty do vody (lopta nie je úplne ponorený): Čím viac je lopta do vody ponorený, tým viac ho musíme tlačiť, aby sa vo vode udržal, prípadne sa ponoril hlbšie. Lopta je úplne ponorený vo vode: sila, ktorú musíme tlačiť loptu do vody, sa nemení.
Pr. 2: Nakresli obrázok čiastočne ponoreného lopty, ktorý tlačí ruka pod vodu. Aké sily na lopta pôsobí?
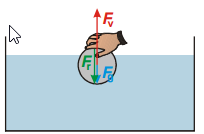
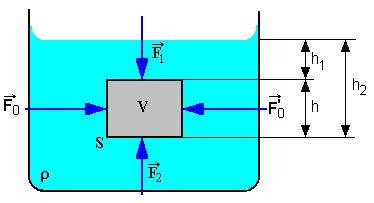
Na loptu pôsobí smerom dole dve sily: gravitačná sila a sila ruky ⇒ na loptu musí pôsobiť ešte sila vody, ktorá ho tlačí proti ruky a proti gravitácii smerom nahor. Sila vody sa označuje ako vztlaková sila.
Na predmety ponorené do kvapaliny pôsobí vztlaková sila
Pr. 3: Lopta na vode pláva, pretože na neho voda pôsobí vztlakovou silou. Pôsobí voda aj na predmety, ktoré neplávajú?
Kameň je pod vodou ďaleko ľahšie ako na vzduchu. Vo vode unesie aj dospelého človeka (Keď sa šikovne položí).
Pr. 4: Chová sa voda pri nadľahčovanie neplavoucích predmetov podobne ako u lopty (jej vztlaková sila sa zväčšuje s ponorením predmetu)? Uveď príklad z vlastnej skúsenosti. Zaliezajú do rybníka. Kamienky na dne nás tlačí čoraz menej, nakoniec tlačiť prestanú a
začneme sa vo vode vznášať ⇒ voda nás nadľahčuje.
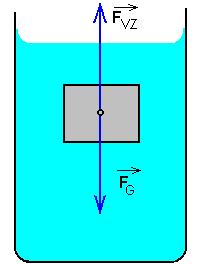
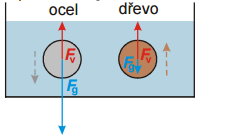
Pr. 5: Na obrázku je nakreslená sivá gulička. Je úplne ponorená do vody a je vyrobená tak, že sa vo vode vznáša (ani nestúpa k hladine, ani neklesá ku dnu). Aké sily na ňu pôsobí? Zakreslite ich do obrázka. Napravo od šedej guličky je naznačená vo vode vo rovnakej hĺbke rovnako veľká myslená guľa z vody (môžeš si predstaviť, že je od ostatné vody oddelená tenkou blankou, ktorá prakticky nič neváži). Ako sa „vodná“ gulička pohybuje? Aké sily pôsobia na nej pôsobí?
Na šedú guličku pôsobia dve sily – gravitačná sila Fg smerom nadol a vztlaková sila vodysmerom nahor. Ak sa guľôčka vznáša a nepohybuje sa, musia byť obe sily rovnako veľké (aby sa navzájom odpočítali).
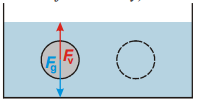
Vodné gulička sa nepohybuje (voda nemôže ani padať ani stúpať vo vode). pôsobí tiež gravitačná sila a vztlaková sila od okolia vody a obe tieto sily musia mať rovnakú veľkosť.
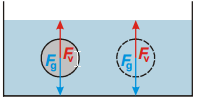
Pr. 6: Porovnaj veľkosti vztlakových síl v predchádzajúcom príklade. Ktoré sily a prečo majú rovnakú veľkosť ako vztlaková sila na šedú guličku?
Obe vztlakovej sily (na šedú aj na vodnej guľôčku). Sú rovnaké (keby sme ich zabalili do tenkého igelitu, voda to nemôže spoznať).
Veľkosť vztlakovej sily na šedú guličku je rovnaká ako veľkosť:
• gravitačné sily na šedú guličku (pretože sivá gulička sa nepohybuje),
• vztlakovej sily na vodné guličku (obe rovnaké a úplne ponorené),
• gravitačné sily na vodné guličku (je rovnako veľká ako vztlaková sila na vodnej guľôčku).
Zhrnieme si pozorovanie z predchádzajúcich dvoch príkladov. Voda nepozná, z akého materiálu je predmet, ktorý sme do nej ponorili. Keby bol z vody, musela by ho nadľahčovať rovnakú silou, akú gravitácia vodné predmet priťahuje k nadol ⇒ voda nadľahčuje predmety rovnakú silou, akú gravitácie by gravitácia priťahovala ich ponorenú časť vyrobenú z vody.
Vodnému telesu, ktoré by bola na mieste ponorenej časti predmetu sa občas hovorí Archimedovom teleso podľa starogréckeho vedca Archimeda, a ktorý tento zákon objavil.
Kvapalina nadľahčuje teleso silou, ktorá sa rovná sile, ktorú by gravitácia priťahovala Archimedovom teleso z rovnakej kvapaliny.
Dodatok: Bežne sa Archimedov zákon udáva v nasledujúcom znení: Teleso ponorené do kvapaliny je nadľahčované silou, ktorá sa rovná váhe kvapaliny telesom vytlačenej. Ťarchou je v tomto znení označovaná sila veľmi blízka a len málo sa líšiaci od gravitačné sily (my zatiaľ rozdiel medzi týmito dvoma silami zanedbávame), kvapalina telesom vytlačená predstavuje Archimedovom teleso.
Pr. 7: Na obrázkoch je nakreslené postupné ponáranie lopty do vody. Vyfarbi u každého okamihu Archimedovom teleso a vysvetli, prečo je vztlaková sila, ktorú voda vytláča loptu, pri väčšom ponorení väčší.
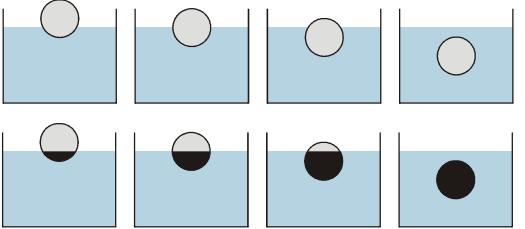
Väčšia ponorenie do vody ⇒ väčšej Archimedovom teleso ⇒ väčšia myslená gravitačná sila na Archimedovom teleso ⇒větší vztlaková sila vody na loptu.
Pr. 8: On obrázkoch sú nakreslené rôzne predmety. Číslo u každého z nich udáva jeho objem. Akú vztlakovou silou bude každý z nich nadľahčovať voda, keď je úplne ponoríme? Akou silou ich budeme musieť do zatlačovať, aby zostali úplne ponorené?
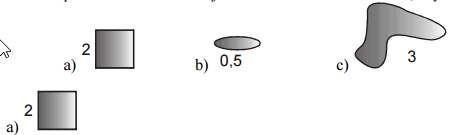
Objem 2 litre ⇒ Archimedovom teleso by obsahovalo 2 litre vody ⇒ Archimedovom teleso by malo hmotnosť 2 kg ⇒ gravitácie by Archimedovom teleso priťahovala silou 2 * 10 = 20 N ⇒ voda by Archimedovom teleso nadlehčovala silou 20 N ⇒ voda bude nadľahčovať predmet silou 20 N.
Silu, ktorú by sme ho museli držať pod vodou spočítať nemôžeme, pretože poznáme iba silu, ktorá teleso tlačí hore, ale nevieme, ako veľká je gravitácia, ktorá ho ťahá nadol.
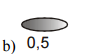
Objem 0,5 litra ⇒ Archimedovom teleso by obsahovalo 0,5 litra vody ⇒ Archimedovom teleso by malo hmotnosť 0,5 kg ⇒ gravitácie by Archimedovom teleso priťahovala silou 0,5 * 10 = 5 N ⇒ voda by Archimedovom teleso nadlehčovala silou 5 N ⇒ voda bude nadľahčovať predmet silou 5 N.
Silu, ktorú by sme ho museli držať pod vodou spočítať nemôžeme, pretože poznáme iba silu, ktorá teleso tlačí hore, ale nevieme, ako veľká je gravitácia, ktorá ho ťahá nadol.
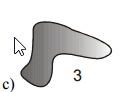
Objem 3 litre ⇒ Archimedovom teleso by obsahovalo 3 litre vody ⇒ Archimedovom teleso by malo hmotnosť 3 kg ⇒ gravitácia by Archimedovom teleso priťahovala silou 3 * 10 = 30 N ⇒ voda by Archimedovom teleso nadlehčovala silou 30 N ⇒ voda bude nadľahčovať predmet silou 30 N.
Silu, ktorú by sme ho museli držať pod vodou spočítať nemôžeme, pretože poznáme iba silu, ktorá teleso tlačí hore, ale nevieme, ako veľká je gravitácia, ktorá ho ťahá nadol.
Pr. 9: Máme k dispozícii k dispozícii predmet, ktorý vo vode klesá ku dnu, silomer, nádobu, dostatok vody a merací valec. Navrhni pokus, ktorým overíme platnosť Archimedovho zákona.
Zavesíme predmet na silomer ⇒ zmeriame gravitačnú silu. Ponoríme predmet zavesený na silomeru do vody ⇒ zmeriame silu. Rozdiel zmeraných síl sa rovná vztlakovej sile (ponorený predmet nadľahčuje voda a preto nepôsobí na silomer tak veľkou silou).
Zmeriame objem, spočítame hmotnosť Archimedovho telesa a silu, ktorou ho priťahuje Zeme.
Výsledok by sa mal rovnať rozdielu nameraných síl.
Pr. 10: Vo vode sú úplne ponorené dve rovnako veľké guľôčky. Jedna železná, druhá drevená. Pôsobí na obe rovnako veľká vztlaková sila vody? Čo sa stane, keď je pustíme? Prečo?
Guličky sú rovnaké ⇒ ich Archimedovom teleso je rovnaké ⇒ pôsobí na ne rovnako veľká vztlaková sila.
Keď je pustíme:
• železná gulička klesne na dno (je ťažká ⇒ pôsobí na nej veľká gravitačná sila, ktorá premôže vztlakovú silu vody),
• drevená gulička vypláva na hladinu (je ľahká ⇒ pôsobí na nej malá gravitačná sila, ktorú premôže vztlaková sila).
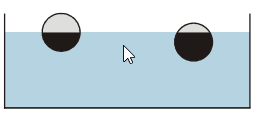
 Pr. 11: Na hladine plávajú dve rovnako veľké guľôčky. Druhá je ponorená menej ako prvý. Ktorá z nich má menšiu hmotnosť?
Pr. 11: Na hladine plávajú dve rovnako veľké guľôčky. Druhá je ponorená menej ako prvý. Ktorá z nich má menšiu hmotnosť?
Obe guličky plávajú ⇒ u oboch je vyrovnaná vztlaková sila s gravitačnou silou.
Druhá gulička je ponorená menej ⇒ má menšiu Archimedovom teleso ⇒ pôsobí na ňu menšie vztlaková sila ⇒ pôsobí na nej menšie gravitačná sila ⇒ je ľahšia.
Pr. 12: Čo je potrebné začať robiť, keď sa človek začne kúriť?
Musíme zväčšiť vztlakovú silu, ktorá nás tlačí nahor ⇒ musíme ponoriť väčšiu časť svojho tela do vody, aby sme zväčšili svoje Archimedovom teleso.
Dodatok: Inštinktívne však topiaci postupuje presne opačne: snaží sa z vody dostať čo najväčšiu časť svojho tela ⇒ zmenšuje svoje Archimedovom teleso a tým aj vztlakovú silu vody ⇒ skôr sa unaví ⇒ skôr sa utopí.
Zhrnutie: Voda nadľahčuje ponorené predmety, pretože by musela dokázať udržať vodu, ktorá by bola na ich mieste.
Kto nám môže šliapnuť na nohu – príklady
Pr. 1: Slon africký býva vysoký až 4 m a váži aj cez 7000 kg. Žirafa síce meria až 6 m, ale pretože je štíhla, váži obyčajnou desatinu toho, čo slon. Je horšie, keď ti šliapne na nohu slon alebo žirafa?
Pr. 2: Skús nájsť dôvod, prečo by obvyklý odhad, že šliapnutia slona je ďaleko horšie, mohol byť nesprávny.
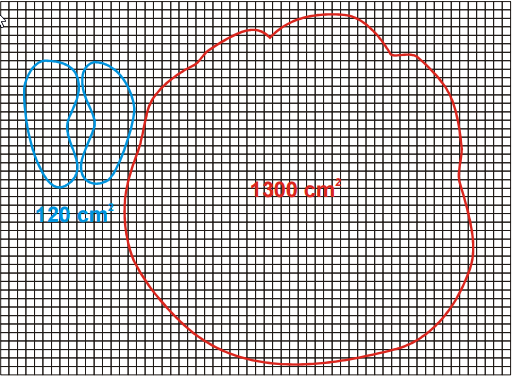
Pr. 3: Urči, akou silou pôsobí na 2
1cm žirafa a akou silou pôsobí slon.
Pr. 4: Sformulujte poučenia, ktoré plynie z premýšľania o slonovi a žirafe.
Pr. 5: Čí stopy sa otlačiť do pôdy hlbšie – žirafy alebo slona?
Pr. 6: Prečo majú horské bicykle hrubšie pneumatiky než kolesá cestné?
Pr. 7: Prečo sa ostrým nožom reže ľahšie než tupým?
Pr. 8: Čím sa líšia nohy sliepky a kačice? Prečo?
Pr. 9: Skús vymyslieť, ako s vybavením dostupným v škole, demonštrovať tlak vyvolaný slonom.
Pr. 10: Akým tlakom tlačíš na podlahu, keď sa houpáš na stoličke?
Pr. 11: Odhadni výpočtom, ako veľkým tlakom pôsobíš na sneh, keď si nazuješ lyže. ako veľkým tlakom pôsobíš na ľad, keď ideš na korčuliach?
Domáce bádania: Navrhni a pokus sa zostrojiť simulátor „slonieho tlaku“.
Kto nám môže šliapnuť na nohu
Pomôcky: milimetrové papiere, ceruzka
Pr. 1: Slon africký býva vysoký až 4 m a váži aj cez 7000 kg. Žirafa síce meria až 6 m, ale pretože je štíhla, váži obyčajnou desatinu toho, čo slon. Je horšie, keď ti šliapne na nohu slon alebo žirafa?
Zrejme slon, pretože je ďaleko ťažšie ako žirafa.
Pr. 2: Skús nájsť dôvod, prečo by obvyklý odhad, že šliapnutia slona je ďaleko horšie, mohol byť nesprávny. Keď nám niekto šliapne na nohu, nezáleží len na tom, ako je ťažký ale aj na tom, ako je
obutý. Čím má väčšiu nohu, tým viac sa jeho sila rozkladá a pôsobí menej (ako keď si stúpneme do snehu v topánkach alebo v lyžiach).
Poriadnu predstavu o tom, ako pôsobí slon alebo žirafa na zem získame až vo chvíli, keď budeme vedieť, aká veľká sila pripadá na kúsok plochy (napríklad 2 cm) ⇒ potrebujeme poznať
plochu nôh žirafy a slona.
Pedagogická poznámka: V triede sa zvyčajne spustí diskusia o tom, ako by sa dala plocha nôh zmerať. Nie je vhodné ju stopnúť príliš rýchlo, ale nemala by trvať ani príliš dlho. Na obrázku sú nakreslené kopýtka žirafy a noha slona na štvorcovej sieti s veľkosťou
štvorčeka 1 cm².

Pr. 3: Urči, akou silou pôsobí na 1cm² žirafa a akou silou pôsobí slon.
žirafa
Hmotnosť 700 kg ⇒ gravitačná sila Fg = mg = 700 * 10 = 7000 N.
Plocha kopýtok: 4 * 120 = 480 cm²
480 cm²… 7000N
1 cm² …7000 : 480 = 14,6 N / cm²
Slon
Hmotnosť 7000 kg ⇒ gravitačná sila Fg = mg = 7000 * 10 = 70000 N.
Plocha kopýtok: 4 * 1300 = 5200 cm²
5200 cm … 70000 N
1 cm² …70000 : 5200 = 13,5 N / cm²
Slon má ďaleko väčšiu plochu nôh, preto na každý centimeter plochy pôsobí menšou silou ako žirafa, ktorá je síce ďaleko ľahší, ale jej kopýtka majú ešte ďaleko menšiu plochu.
Pr. 4: Sformulujte poučenia, ktoré plynie z premýšľania o slonovi a žirafe. Následky pôsobenia sily nezávisí len na jej veľkosti, ale aj na veľkosti plochy, na ktorá sila pôsobí.
Následky pôsobenia sily nezávisí len na jej veľkosti, ale aj na veľkosti
plochy, na ktorú pôsobí. Sile, ktorá pôsobí na každý kúsok plochy (napríklad cm²), hovoríme tlak, značíme ju písmenkom p.
Pr. 5: Čí stopy sa otlačiť do pôdy hlbšie – žirafy alebo slona?
Žirafa pôsobí na zem väčším tlakom ⇒ jej stopy budú hlbšie ako stopy slona.
Pr. 6: Prečo majú horské bicykle hrubšie pneumatiky než kolesá cestné? Horské bicykle slúži aj na pohyb v teréne ⇒ aby sa neprepadala do mäkkej pôdy, musí pôsobiť na zem čo najmenším tlakom ⇒ musí doliehať na zem väčšou plochou.
Pr. 7: Prečo sa ostrým nožom reže ľahšie než tupým?
Ostrý nôž sa dotýka predmetu na malej ploche ⇒ pôsobí obrovským tlakom (aj pri malej sile) ⇒ ľahko naruší predmet a rozreže ho.
Pr. 8: Čím sa líšia nohy sliepky a kačice? Prečo?
Kačica má medzi prstami blanu ⇒ väčšia plocha nôh ⇒ menší tlak na podložku ⇒ kačica sa neprepadá ani v bahne na brehu rybníka.
Ďalším dôvodom pre väčšiu plochu nôh je ich využitie pre plávanie vo vode.
Pr. 9: Skús vymyslieť, ako s vybavením dostupným v škole, demonštrovať tlak vyvolaný slonom.
Môžeme zaťažiť nejaký predmet s malou plochou tak, aby pôsobil tým správnym tlakom a položiť si ho na ruku.
Pedagogická poznámka: Žiaci najskôr tvrdí, že bude potrebné niečo veľké a ťažkého, ale za chvíľku určite niekto príde na to, že stačí dostatočne malá plocha a vystačíme aj s malou hmotnosťou.
Pr. 10: Akým tlakom tlačíš na podlahu, keď sa houpáš na stoličke?
Musíme poznať plochu nohy u stoličky.
Plocha jednej nohy u stoličky: 2
1 cm² ⇒ dve nohy 2 cm².
Hmotnosť 78 kg ⇒ gravitačná sila Fg = mg = 78 * 10 = 780 N.
![]()
Pri húpanie na stoličke, pôsobím na podlahu tlakom 390 N / cm².
Pr. 11: Odhadni výpočtom, ako veľkým tlakom pôsobíš na sneh, keď si nazuješ lyže. ako veľkým tlakom pôsobíš na ľad, keď ideš na korčuliach? Potrebnej veľkosti odhadni. Musíme odhadnúť plochu lyží aj plochu korčúľ.
Lyže (zjazdové): dĺžka 170 cm, šírka 9 cm.
Plocha lyží:
2 * 170 * 9 = 3060 cm²
Tlak: 780 : 3060 = 0, 25 N / cm²
Korčule: dĺžka 25 cm, šírka 0,3 cm.
Plocha korčulí: 2 * 25 * 0,3 =15 cm²
Tlak: 780 : 15 = 52 N / cm²
Pri jazde na lyžiach pôsobíme na sneh tlakom 2
0,25 N / cm, pri korčuľovaní pôsobíme na ľad tlakom 52 N / cm².
Domáce bádania: Zisti, čo nepresnejšie, akým tlakom pôsobíš bosý na zem. hľadaj čo najpresnejšie a najjednoduchšie postup. Rada: Môžeš využiť milimetrový papier alebo presné váhy.
Domáce bádania: Navrhni a pokus sa zostrojiť simulátor „slonieho tlaku“.
Dodatok: Obrázky stop prevzaté z učebnice Fyzika okolo nás pre 6. ročník, Rojko a kol. Scientia.
Zhrnutie: Nezáleží len na veľkosti sily, ale aj na ploche, na ktorú sila pôsobí.
Meranie spotreby domácich spotrebičov
Spotrebiče s veľkou spotrebou
Varná kanvica: Spotreba 1826 W, po spustení je spotreba o trochu vyšší (1995 W) potom klesá a kolíše okolo 1880 W.

Mikrovlnná rúra: Spotreba 1449 W.
Dve zaujímavosti:
• wattmeter neukazuje žiadnu spotrebu, keď rúra nepracuje, hoci svieti display a beží hodiny,
• spotreba nezávisí na tom, na koľko percent je zapnutý mikrovlnný výkon.

Rúra: Pri zapnutom vetranie a obojstrannom ohrevu je spotreba 2300 W (2,3 kW), vypnutím vetráku sa zníži o 100 W. Rúra odoberá elektrický prúd aj vo vypnutom stravu (bežia hodiny na display) a to 2,7 W.

Spotrebiče s malou spotrebou
CD prehrávač: Prehrávanie 10 W.
Zaujímavosť:
• vypnutý prehrávač odoberá zo siete 2,2 W, hoci mu nesvieti display, nebeží hodiny ani nesvieti kontrolná LED dióda.

Televízia (stará CRT – s vákuovou obrazovkou): Spustená televízia 57,7 W (hodnoty kolíšu medzi 40 W a 60 W), vypnutá televízia (svietiace LED) 7 W.

Lampička s úspornou žiarivkou: Zapnutá lampička 13,3 W (krátko po zapnutí len 10,8 W, potom spotreba stúpa k 14,8 W a potom klesá na 13 W, kde potom zostáva bezo zmeny).

Záver
Väčšiu spotrebu elektrickej energie majú prístroje, ktoré vyrábajú teplo.
Meranie spotreby domácich spotrebičov – príklady
Pr. 1: Zmeraj pomocou wattmetra okamžitú spotrebu (výkon) troch spotrebičov s veľkou spotrebou a troch spotrebičov s malou spotrebou. Zapíš namerané hodnoty a skontroluj, či prístroje s predpokladanou nižšou spotrebou naozaj spotrebúvajú menej ako
prístroje s vyššou spotrebou. Pokiaľ u nejakého spotrebiča naměříš niečo zaujímavé, zapíš to. Každý prístroj kúp fotografiu wattmetra ukazujúceho charakteristickú hodnotu výkonu. Zhotovené fotografie prines do školy k ďalšiemu spracovanie v hodine IKT.
Meranie spotreby domácich spotrebičov
Pomôcky: Vernier WattPro, domáce spotrebiče
Pedagogická poznámka: Táto domáce práce nadväzuje na predchádzajúce domáce prácu – pozorovanie elektromeru, ktorého cieľom bolo vytipovať spotrebiče s veľkou a spotrebiče s malou spotrebou elektrickej energie. Pri spoločnom zhrnutie tohto pozorovania sa žiaci zhodnúť na tom, že veľkú spotrebu energie majú spotrebiče, ktoré vyrábajú teplo (variče, varné kanvice, rúry, mikrovlnné rúry, práčky (pri ohrievaní vody), ďaleko menšie spotrebu potom majú spotrebiče, ktoré nie sú určené na výrobu tepla (lampičky, televízia, počítače, rádiá, prehrávače, hodinky). Domáce pozorovanie tak slúži na overenie týchto
záverov a nácviku pozorovacie schopnosti.
Wattmeter: zariadenie, ktoré merajú energiu odoberané elektrickým spotrebičom. wattmeter pripojíme do zásuvky miesto spotrebiča, spotrebič pripojíme miesto do zásuvky do wattmetra.
Všetka energia, ktorú spotrebič odoberá zo siete, tak prechádza cez wattmeter, ktorý ju môže zmerať. Okamžitú hodnotu vo wattoch zobrazuje na display. Prístroj je možné pripojiť k počítači, ktorý môže hodnoty priebežne programom Logger Lite odčítať a ukladať k ďalšiemu spracovanie.
Pr. 1: Zmeraj pomocou wattmetra okamžitú spotrebu (výkon) troch spotrebičov s veľkou spotrebou a troch spotrebičov s malou spotrebou. Zapíš namerané hodnoty a skontroluj, či prístroje s predpokladanou nižšou spotrebou naozaj spotrebúvajú menej ako
prístroje s vyššou spotrebou. Pokiaľ u nejakého spotrebiča naměříš niečo zaujímavé, zapíš to. Každý prístroj kúp fotografiu wattmetra ukazujúceho charakteristickú hodnotu výkonu. Zhotovené fotografie prines do školy k ďalšiemu spracovanie v hodine IKT.
Spotrebiče s veľkou spotrebou:
• varná kanvica: spotreba 1882 W, po spustení je spotreba o trochu vyšší (1995 W) potom
klesá a kolíše okolo 1880 W.
• Mikrovlnná rúra: spotreba 1470 W. Dve zaujímavosti:
o wattmeter neukazuje žiadnu spotrebu, keď rúra nepracuje, hoci svieti display a beží hodiny, o spotreba nezávisí na tom, na koľko percent je zapnutý mikrovlnný výkon.
• Rúra: Pri zapnutom vetranie a obojstrannom ohrevu je spotreba 2300 W (2,3 kW), vypnutím ventilátora sa zníži o 100 W. Rúra odoberá elektrický prúd aj vo vypnutom stravu (bežia hodiny na display) a to 2,7 W.
Spotrebiče s malou spotrebou:
• Cd prehrávač: prehrávanie 10 W. Zaujímavosť:
o vypnutý prehrávač odoberá zo siete 2,2 W, hoci mu nesvieti display, nebeží hodiny ani nesvieti kontrolná LED dióda.
• Televízia: spustená televízia 45 W, vypnutá televízia (svietiace LED) 7 W.
• Dióda s úspornou žiarivkou: zapnutá lampička 13 W (krátko po zapnutí len 10,8 W, potom spotreba stúpa k 14,8 W a potom klesá na 13 W, kde potom zostáva bezo zmeny.
Pomocou wattmetra sme potvrdili predchádzajúci záver, že najväčšiu spotrebu majú spotrebiče vyrábajúce teplo.
Pedagogická poznámka: Pri kontrole v hodine je okrem záveru dôjsť k tomu, že spotreba rovnakého typu spotrebičov sa môže radikálne líšiť. že väčšina dnešných spotrebičov spotrebováva energiu aj keď je vypnutá (StandBy mód) a že práve v tomto stave je spotreba starších zariadení znateľne vyššie. Záujemcom je dobré dať za úlohu spočítať koľko ročne zaplatí za StandBy mód u nejhladovějšího zariadení (bývajú to stokorunáky).
Zhrnutie: Väčšia spotrebu elektrickej energie majú prístroje, ktoré vyrábajú teplo.
Energia na tanieri – príklady
Napríklad: Na raňajky sme zjedol krajec a pol chleba (80 g), namazaný maslom (odhad 15 g) a trochou jahodovej marmelády (odhad 20 g). Zapil sme ho hrnčekom čaju s lyžičkou cukru. vo
50 g chleba … 510 kJ
1 g chleba … 510 : 50 = 10 kJ
80 g chleba … 80 * 10 = 800 kJ
Pr. 1: dopočítajte energiu obsiahnutú v maslu a marmeláde.
Pr. 2: Spočítaj energiu, ktorú si prijal počas deň, v ktorom si si písal jedálniček.
Pr. 3: Prejdi si zoznam aktivít, ktoré si počas dňa vykonal a spočítame svoj denný výdaj energie.
Domáce bádania: Zisti, aká je Vaša týždenné spotreba energie a výpočtu priemernej dennej
spotrebu domácnosti? Koľko za 1 kWh platíte?